题目内容
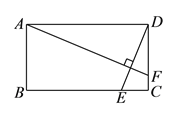
【题目】如图,已知在等腰三角形ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE与BD交于点O.

(1)求证:△BCE≌△CBD;
(2)写出图中所有相等的线段.
【答案】(1)见解析;(2)AB=AC,BE=CD,AE=AD,CE=BD,OB=OC,OE=OD.
【解析】
根据AB=AC,得出∠EBC=∠DCB,在△BCE和△CBD中,根据AAS即可证出△BCE≌△CBD.
证明:(1)∵AB=AC,BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90,
在△ABD和△ACE中,
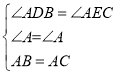 ,
,
∴△ABD≌△ACE(AAS),
∴BD=CE;
∵AB=AC,
∴∠EBC=∠DCB,
在△BCE和△CBD中,
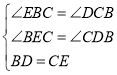 ,
,
∴△BCE≌△CBD.
(2)相等的线段有:AB=AC,BE=CD,AE=AD,CE=BD,OB=OC,OE=OD.

练习册系列答案
相关题目
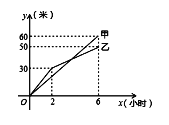
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t分钟,估计当![]() 时,
时,![]() 的值为( )
的值为( )
A. 140B. 200C. 240D. 260