Question

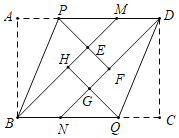
【题目】如图，在矩形纸片ABCD中，BM，DN分别平分∠ABC，∠CDA，沿BP折叠，点A恰好落在BM上的点E处，延长PE交DN于点F沿DQ折叠，点C恰好落在DN上的点G处，延长QG交BM于点H，若四边形EFGH恰好是正方形，且边长为1，则矩形ABCD的面积为____．

Answer 1

【答案】8+6.

【解析】

设CQ＝x，由角平分可以证明△BHQ，△NQG，△PDF都是等腰直角三角形；根据折叠的性质可知：AP＝PE，BE＝AB，CD＝DG，GQ＝CQ；根据边角关系证明△ABP≌△CDQ（ASA）得到AP＝CQ；根据以上证明可以得到边的关系：HQ＝1+x，HB＝1+x，BQ＝（1+x），BC＝+（1+x），CD＝NC＝x+NQ＝x+x，DG＝x+x＝1+DF＝1+1+x，求出x即可求解；

设CQ＝x，

∵矩形ABCD，BM，DN分别平分∠ABC，∠CDA，

∴∠ABM＝∠MBC＝∠CDN＝∠ADN＝45°，

∴△BHQ，△NQG，△PDF都是等腰直角三角形，

∵沿BP折叠，点A恰好落在BM上的点E处，

∴AP＝PE，BE＝AB，

∵点C恰好落在DN上的点G处，

∴CD＝DG，GQ＝CQ，

△ABP≌△CDQ（ASA），

∴AP＝CQ，

∵正方形EFGH边长为1，

∴HQ＝1+x，HB＝1+x，

∴BQ＝（1+x），BC＝+（1+x），CD＝NC＝x+NQ＝x+x，

∴DG＝x+x＝1+DF＝1+1+x，

∴x＝，

∴BC＝2+2，CD＝2+，

∴矩形ABCD的面积＝（2+2）（2+）＝8+6，

故答案为8+6.