题目内容
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 于
于![]() ,交
,交![]() 轴于点
轴于点![]()
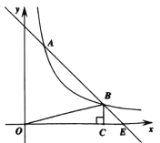
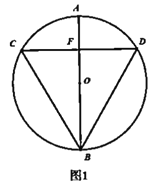
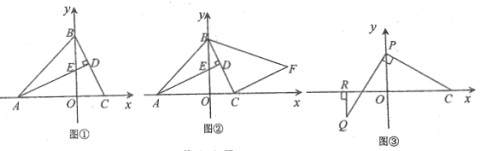
(1)如图①,求点![]() 的坐标;
的坐标;
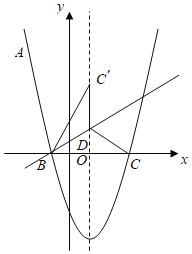
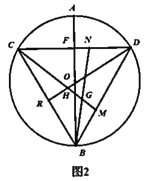
(2)如图②:将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得线段
后得线段![]() ,连接
,连接![]() ,求点
,求点![]() 的坐标;
的坐标;
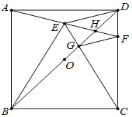
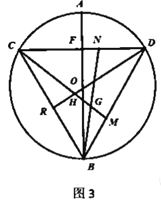
(3)如图③, 点![]() 为
为![]() 轴正半轴上一动点, 点
轴正半轴上一动点, 点![]() 在第二象限内,
在第二象限内,![]() 于
于![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,求
,求![]() 的值.
的值.
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)1
;(3)1
【解析】
(1)根据![]() 得
得![]() 即可求出点C的坐标
即可求出点C的坐标
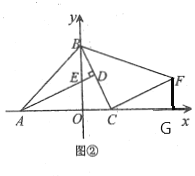
(2)过点![]() 作
作![]() 轴于
轴于![]() ,根据已知条件可得出OC=1,OB=3,只需要证明
,根据已知条件可得出OC=1,OB=3,只需要证明![]() 即可得到F的横纵坐标表示;
即可得到F的横纵坐标表示;
(3)根据已知条件可得四边形![]() 为矩形,得出
为矩形,得出![]() ,
,![]() ,通过角度之间的相互转化可证的
,通过角度之间的相互转化可证的![]() ,得到
,得到![]() ,再根据
,再根据![]() 可得结果
可得结果
解:(1)![]() 点
点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]()
![]()
![]() 于
于![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
(2)由(1)可知![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
过点![]() 作
作![]() 轴于
轴于![]()
![]()
![]()
![]() 线段
线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得线段
后得线段![]() ,
,
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
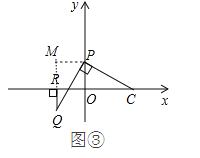
(3)过点![]() 作
作![]() 延长线于点
延长线于点![]()
![]()
![]() 垂直
垂直![]() 轴于点
轴于点![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 为矩形
为矩形
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
【题目】某课外学习小组根据学习函数的经验,对函数![]() 的图象与性质进行了探究请补充完整以下探索过程:
的图象与性质进行了探究请补充完整以下探索过程:
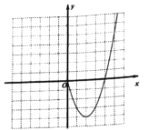
(1)列表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出![]() ________,
________,![]() ________;
________;
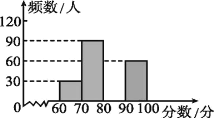
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象,并结合图象写出该函数的两条性质:
性质1______________________________________________________
性质2_______________________________________________________
(3)若方程![]() 有四个不同的实数根,请根据函数图象,直接写出k的取值范围.
有四个不同的实数根,请根据函数图象,直接写出k的取值范围.