题目内容
【题目】已知在四边形![]() 中,
中,![]() ,
,![]() .
.
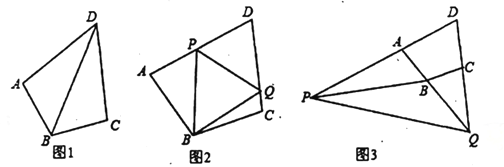
(1)如图1.连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,满足
上,满足![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,如图3所示,仍然满足
的延长线上,如图3所示,仍然满足![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,并给出证明过程.
的数量关系,并给出证明过程.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)根据已知条件得出![]() 为直角三角形,再根据
为直角三角形,再根据![]() 证出
证出![]() ,从而证出
,从而证出![]() ;
;
(2)如图2,延长DC到 K,使得CK=AP,连接BK,通过证△BPA≌△BCK(SAS)得到:∠1=∠2,BP=BK.然后根据![]() 证明得
证明得![]() ,从而得出
,从而得出![]() ,然后得出结论;
,然后得出结论;
(3)如图3,在CD延长线上找一点K,使得KC=AP,连接BK,构建全等三角形:△BPA≌△BCK(SAS),由该全等三角形的性质和全等三角形的判定定理SSS证得:△PBQ≌△BKQ,则其对应角相等:∠PBQ=∠KBQ,结合四边形的内角和是360度可以推得:∠PBQ=90°+![]() ∠ADC.
∠ADC.
(1)证明:如图1,

∵![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中,
中,![]()
∴![]()
∴![]()
(2)如图2,

延长![]() 至点
至点![]() ,使得
,使得![]() ,连接
,连接![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∴![]()
(3)![]()
如图3,在![]() 延长线上找一点
延长线上找一点![]() ,使得
,使得![]() ,连接
,连接![]() ,
,
∵![]()
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中,
中,

∴![]()
∴![]() ,
,![]()
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中,
中,

∴![]()
∴![]()
∴![]()
∴![]()
∴![]() .
.

练习册系列答案
相关题目





