��Ŀ����
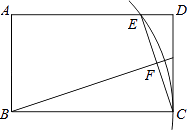
����Ŀ����ͼ��8��8������������ÿ��С�����DZ߳�Ϊ1�������Σ�A��B�Ǹ�㣨�����ߵĽ��㣩��������������ֱ��Ϊ�����ᣬ�������н���ƽ��ֱ������ϵxOy��ʹ��A����Ϊ����2��4����
(1)�������У��������ƽ��ֱ������ϵ��
(2)�ڵڶ������ڵĸ�����ҵ�һ��C��ʹA��B��C���������ABΪ�ױߵĵ��������Σ��������������������C���������� ������������ABC����y��ԳƵġ�A��B��C�䣮

���𰸡�(1)��������(2)����1��1������ͼ������.
��������
��1���ɵ�A����2��4���ɽ���ƽ��ֱ������ϵ��
��2�����ݵ��������εĶ�����ͼ�ɵã��ٷֱ�������A��B��C����y��ĶԳƵ㣬˳�����Ӽ��ɵã�
(1)��ͼ��ʾ������ƽ��ֱ������ϵ��
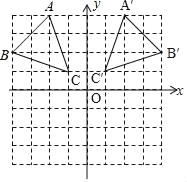
(2)��ͼ��ʾ����ABC��Ϊ�������е�C������Ϊ����1��1������ABC����y��ԳƵġ�A��B��C����ͼ��ʾ��
�ʴ�Ϊ������1��1����

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�����Ŀ��ij��˾Ϊһ�����͵��Ӳ�Ʒ�ڸó��е���Լ�����̣���֪ÿ����Ʒ�Ľ���Ϊ40Ԫ���ù�˾ÿ���������ֲ�Ʒ��������֧�����������ۣ��ܼ�100��Ԫ�������۹����е�֪����������y������������۵���x��Ԫ��֮����������ʾ�ĺ�����ϵ�����ҷ���y��x��һ�κ�����
���۵���x��Ԫ�� | 50 | 60 | 70 | 80 |
��������y������� | 5.5 | 5 | 4.5 | 4 |
��1����y��x�ĺ�����ϵʽ��
��2���ʣ������۵���xΪ��ֵʱ���ù�˾������������������ֵ��
����ע��������=�����۶�ܽ����۩�������֧��
��3������˾ϣ����������60��Ԫ����������ù�˾ȷ�����۵��۵ķ�Χ��