��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���B��a��b���ǵ�һ������һ�㣬��a��b�����ʽa2-6a+9+|b-1|=0��

��1�����B�����ꣻ
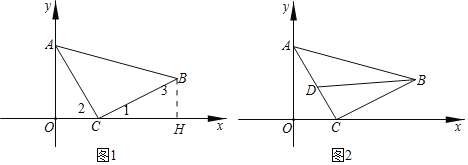
��2����ͼ������C��ÿ��1����λ���ȵ��ٶȴ�O���������x��������᷽���˶���ͬʱ����A��ÿ��2����λ���ȵ��ٶȴ�O���������y��������᷽���˶������˶���ʱ��Ϊt�룬��tΪ��ֵʱ����ABC��ABΪб�ߵĵ���ֱ�������Σ�
��3����ͼ���ڣ�2���������£�����ABC��ƽ����BD����BD�ij�Ϊm����ADB�����ΪS�����ú�m��ʽ�ӱ�ʾS��
���𰸡���1��B��3��1������2����t=1ʱ����ABC����ABΪб�ߵĵ���ֱ�������Σ���3��![]()
��������
��1�����ݷǸ��Եó�a��b��ֵ��������ɣ�
��2����B��BH��x����H�����ݵ���ֱ�������ε����ʺ�ȫ�������ε��ж������ʽ�ɣ�
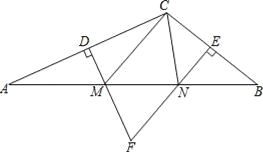
��3������A��AF��DB����BD�ӳ�����F��AF�ӳ��߽�BC���ӳ����ڵ�E������ȫ�������ε��ж������ʽ�ɣ�
�⣺��1����a2-6a+9+|b-1|=0��
�ࣨa-3��2+|b-1|=0
�ң�a-3��2��0��|b-1|��0
��a-3=0��b-1=0
��a=3��b=1
��B��3��1����
��2����B��BH��x����H
��B��3��1����
��BH=1
�������OA=2t��OC=t
�ߡ�ACB����ABб�ߵĵ���ֱ��������
��AC=BC��
��ACB=90��
���1+��2=90��
��BH��x�ᣬ
���OHB=90��
���1+��3=90��
���2=��3
���AOC=��CHB=90��
����AOC����CHB��
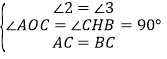 ��
��
���AOC�ա�CHB��AAS��
��OC=BH
��t=1��
�൱t=1ʱ����ABC����ABΪб�ߵĵ���ֱ�������Σ�
��3������A��AF��DB����BD�ӳ�����F��AF�ӳ��߽�BC���ӳ����ڵ�E��

�ߡ�AFB=��ACB=90��
���1+��E=90��
��2+��E=90��
���2=��1
����DCB����ECA��
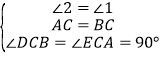 ��
��
���DCB�ա�ECA��ASA��
��AE=DB=m
����BFA����BFE��
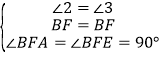 ��
��
���BFA�ա�BFE��ASA��
��AF=EF=![]()
��![]() ��
��