Question

【题目】如图，在平面直角坐标系中，半径为1的⊙A的圆心与坐标原点O重合，线段BC的端点分别在x轴与y轴上，点B的坐标为（6，0），且sin∠OCB= ．

（1）若点Q是线段BC上一点，且点Q的横坐标为m．
①求点Q的纵坐标；（用含m的代数式表示）
②若点P是⊙A上一动点，求PQ的最小值；
（2）若点A从原点O出发，以1个单位/秒的速度沿折线OBC运动，到点C运动停止，⊙A随着点A的运动而移动．
①点A从O→B的运动的过程中，若⊙A与直线BC相切，求t的值；
②在⊙A整个运动过程中，当⊙A与线段BC有两个公共点时，直接写出t满足的条件．

Answer 1

【答案】
（1）解：①∵点B的坐标为（6，0），tan∠OCB= ，

∴BC=10，OC=8，

设直线BC的解析式为y=kx+b，

，

解得 ，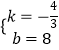

∵点Q的横坐标为m，

∴点Q的纵坐标为﹣ m+8；

②如图1，作OQ⊥AB交⊙A于P，则此时PQ最小，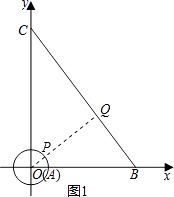

×AB×OQ= ×BO×CO，

解得，OQ=4.8，

∴PQ最小=OQ最小﹣1=3.8；

（2）解：①如图2，⊙A与直线BC相切于H，

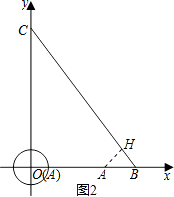
则AH⊥BC，又∠BOC=90°，

∴△BHA∽△BOC，

∴ ，即 ，

解得，BA= ，

则OA=6﹣ = ，

∴t= 时，⊙A与直线BC相切；

②由（2）①得，t= 时，⊙A与直线BC相切，

当t=5时，⊙A经过点B，

当t=7时，⊙A经过点B，

当t=15时，⊙A经过点C，

故 ＜t≤5或7≤t≤15时，⊙A与线段BC有两个公共点．

【解析】(1)①根据待定系数法确定直线BC的解析式，即写出Q点的纵坐标。②作OQ⊥AB交⊙A于P，则此时PQ最小，根据两点之间线段最短进行分析。
（2）①根据相切得垂直，即可得出△BHA∽△BOC，然后求出AB的长，得OA的长，即可得出时间t；②由点动带动图形动，对题意进行分析，有两个交点即分类型讨论，由正好一个交点，过渡到正好两个交点的方式思考。
【考点精析】本题主要考查了确定一次函数的表达式和直线与圆的三种位置关系的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．