题目内容
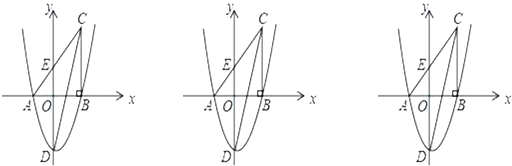
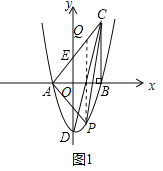
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线![]() 经过A、B两点,与y轴交于点D(0,﹣6).
经过A、B两点,与y轴交于点D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(3)若点M是x轴正半轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)N
;(3)N![]()
【解析】
(1)先确定B(4,0),再利用待定系数法求出抛物线解析式为y= ![]() ;
;
(2)先利用待定系数法求得直线AC的解析式为y= ![]() ,作PQ∥y轴交AC于Q,设P(m,
,作PQ∥y轴交AC于Q,设P(m,![]() ),则Q(m,
),则Q(m,![]() ),则PQ=
),则PQ= ![]() ,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
(3)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,根据角平分线的性质得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,则F(4,3),接着求出直线AF的解析式为y=![]() x+1,于是通过解方程组
x+1,于是通过解方程组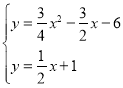 得N点坐标为(
得N点坐标为(![]() )
)
(1)∵BC⊥x轴,点C(4,8),
∴B(4,0),
把B(4,0),D(0,-6)代入y=![]() 得
得![]() ,解得
,解得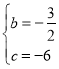
∴抛物线解析式为![]()
(2)设直线AC的解析式为y=px+q,
把A(-2,0),C(4,8)代入得![]() ,解得
,解得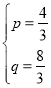
∴直线AC的解析式为![]()
如图1,作PQ∥y轴交AC于Q,
设![]() ,则Q
,则Q![]()
![]()
![]()
(3)图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,则FH=FB,
易得AH=AB=6,
![]()
![]()
![]()
![]()
∴F(4,3),
易得直线AF的解析式为![]()
解方程组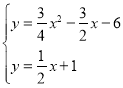 得
得![]() 或
或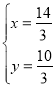
∴N点坐标为![]()


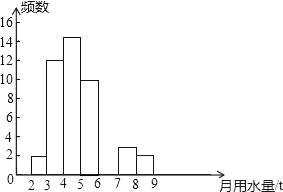
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.