Question

【题目】对于平面直角坐标系xOy中的任意两点M，N，给出如下定义：点M与点N的“折线距离”为：．

例如：若点M(-1，1)，点N(2，-2)，则点M与点N的“折线距离”为：．根据以上定义，解决下列问题：

（1）已知点P(3，-2)．

①若点A(-2，-1)，则d(P，A)= ；

②若点B(b，2)，且d(P，B)=5，则b= ；

③已知点C（m,n）是直线上的一个动点，且d(P，C)<3，求m的取值范围．

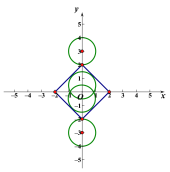
（2）⊙F的半径为1，圆心F的坐标为(0，t)，若⊙F上存在点E，使d(E，O)=2，直接写出t的取值范围．

Answer 1

【答案】（1）① 6，② 2或4，③ 1＜m＜4；（2）或.

【解析】

（1）①根据“折线距离”的定义直接列式计算；

②根据“折线距离”的定义列出方程，求解即可；

③根据“折线距离”的定义列出式子，可知其几何意义是数轴上表示数m的点到表示数3的点的距离与到表示数2的点的距离之和小于3.

（2）由题意可知，根据图像易得t的取值范围．

解：（1） ①

②

∴

∴ b=2或4

③ ，

即数轴上表示数m的点到表示数3的点的距离与到表示数2的点的距离之和小于3，所以1＜m＜4

（2）设E（x,y），则，

如图，若点E在⊙F上，则.