Question

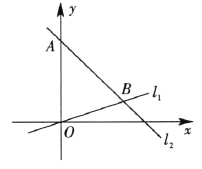
【题目】如图1，在四边形ABCD的边BC的延长线上取一点E，在直线BC的同侧作一个以CE为底的等腰△CEF，且满足∠B+∠F＝180°，则称三角形CEF为四边形ABCD的“伴随三角形”．

（1）如图1，若△CEF是正方形ABCD的“伴随三角形”：

①连接AC，则∠ACF＝　 　；

②若CE＝2BC，连接AE交CF于H，求证：H是CF的中点；

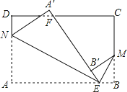
（2）如图2，若△CEF是菱形ABCD的“伴随三角形”，∠B＝60°，M是线段AE的中点，连接DM、FM，猜想并证明DM与FM的位置与数量关系．

Answer 1

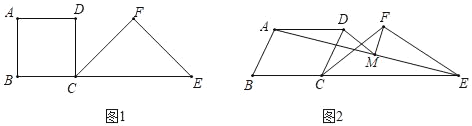
【答案】（1）①90°；②见解析；（2）DM＝FM，理由见解析

【解析】

（1）①连接AC，利用正方形的性质得到∠ACB=45°，再利用等腰直角三角形的性质得到∠FCE=45°，然后利用∠ACF+∠ACB+∠FCE=180°进行求解即可；

②设BC＝a，则CE＝2a，利用等腰直角三角形的判定及性质得到AC=EF，然后利用全等三角形的判定及性质以及中点的定义进行求证即可；

（2）延长DM交BE于G，连接FM，FG，根据△CEF是菱形ABCD的“伴随三角形”，∠B＝60°，得到△CEF是等腰三角形，且∠CFE＝120°，然后利用全等三角形的判定及性质进行求解即可.

解：（1）①连接AC，

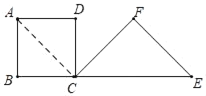
∵四边形ABCD是正方形

∴∠ACB＝45°，∠B＝90°，

∵△CEF是正方形ABCD的“伴随三角形”，

∴∠B+∠F＝180°，

∴∠F＝90°，

又∵△CFE是等腰三角形，

∴∠FCE＝45°，

∴∠ACF＝180°﹣∠FCE﹣∠ACB＝90°，

故答案为：90°；

②连接AE，交CF于点H，

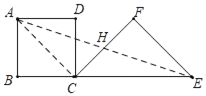
∵CE＝2BC，

∴设BC＝a，CE＝2a，

∵∠B＝90°，AB＝BC＝a，

∴AC＝a，

∵∠F＝90°，CE＝2a，

∴EF＝FC＝a，

∵∠ACF＝∠F＝90°，

∴AC∥EF，

∴△ACH∽△EFH，

∴，

∴CH＝HF，

∴点H是CF的中点，

（2）DM＝FM，FM⊥DM

理由如下：如图，延长DM交CE于点P，连接DF，FP，

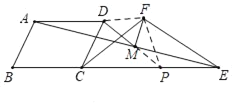
∵四边形ABCD是菱形

∴AB＝BC＝CD＝AD，AB∥CD，AD∥BC，

∴∠B＝∠DCP＝60°，∠DAM＝∠PEM，

∵若△CEF是菱形ABCD的“伴随三角形”，∠B＝60°，

∴∠CFE+∠B＝180°，

∴∠CFE＝120°，且△CEF是等腰三角形，

∴∠ECF＝30°＝∠FEC，CF＝EF，

∴∠DCF＝30°

∵∠DAM＝∠PEM，AM＝ME，∠AMD＝∠PME，

∴△ADM≌△EPM（ASA），

∴AD＝PE，DM＝MP，

∴CD＝PE，且CF＝EF，∠DCF＝∠FEC＝30°，

∴△CDF≌△EPF（SAS），

∴DF＝PF，∠DFC＝∠PFE，

∵∠PFE+∠CFP＝∠CFE＝120°，

∴∠DFC+∠CFP＝120°＝∠DFP，且DF＝FP，DM＝PM，

∴FM⊥DM，∠FDM＝30°，

∴DM＝FM.