题目内容
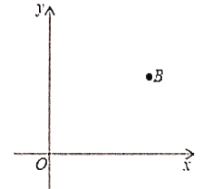
【题目】如图,平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() .
.
(1)请用直尺(不带刻度)和圆规作一条直线![]() ,它与
,它与![]() 轴和
轴和![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() 和点
和点![]() ,且
,且![]() 与
与![]() 关于直线
关于直线![]() 对称.(作图不必写作法,但要保留作图痕迹.)
对称.(作图不必写作法,但要保留作图痕迹.)
(2)请求出(1)中作出的直线![]() 的函数表达式.
的函数表达式.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)作线段OB的垂直平分线,与![]() 轴和
轴和![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() 和点
和点![]() ,直线AC即是所求的直线.
,直线AC即是所求的直线.
(2)由(1)可得:AC垂直平分OB,则OA=AB,可设OA=x,则AB=x,AF=6-x,BF=4,根据勾股定理列出方程,解得x的值,即可求出A点坐标;根据同角的余角相等可得![]() ,利用
,利用![]() ,代入数值即可求得OC的长,得到C点的坐标,根据A、C两点坐标,用待定系数法求直线AC的解析式即可;
,代入数值即可求得OC的长,得到C点的坐标,根据A、C两点坐标,用待定系数法求直线AC的解析式即可;
(1)作图如下:
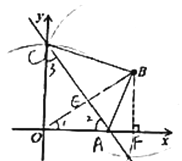
直线AC即是所求的直线.
(2)设![]() 与
与![]() 相交于点
相交于点![]() ,
,
过![]() 作
作![]() 轴于
轴于![]() ,
,
∵![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
∴![]() .
.
∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,
![]() ,
,
∴![]() ,
,
解得![]() .
.
∴点![]() 坐标为
坐标为![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
设:![]() ,则
,则
![]() ,
,
![]() .
.
解得:![]() ,
,
![]() .
.
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目