��Ŀ����
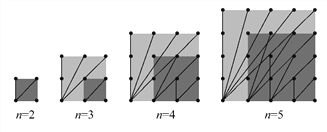
����Ŀ��̽��n��n�������ζ��Ӱ���(n�Ƕ��Ӱ�ÿ���ϵĶ�����,ÿ�������ڶ��Ӽ�ľ���Ϊ1),�������������������õ��IJ�ͬ����ֵ���߶�����:
��n=2ʱ,���Ӱ���������ͬ�߶εij���ֵֻ��1��![]() �����Բ�ͬ����ֵ���߶�ֻ��2��,����S��ʾ��ͬ����ֵ���߶�����,��S=2;
�����Բ�ͬ����ֵ���߶�ֻ��2��,����S��ʾ��ͬ����ֵ���߶�����,��S=2;
��n=3ʱ,���Ӱ���������ͬ�߶εij���ֵֻ��1, ![]() ��2,
��2, ![]() ��2
��2![]() ����,��n=2ʱ������3��,��S=2+3=5.
����,��n=2ʱ������3��,��S=2+3=5.
(1)�۲�ͼ��,��д�±�:
������(n��n) | Sֵ |
2��2 | 2 |
3��3 | 2+3 |
4��4 | 2+3+��____�� |
5��5 | ��________�� |
(2)д��(n-1)��(n-1)��n��n���������Ӱ���,��ͬ����ֵ���߶�����֮��Ĺ�ϵ;(��ʽ�ӻ����Ա�������).
(3)��n��n�Ķ��Ӱ�,д����n��ʾS�Ĵ���ʽ.
���𰸡� 4 2+3+4+5(��14)
�������������������1��������Ϊ2��2ʱ�����в�ͬ���߶�2����
������Ϊ3��3ʱ�����в�ͬ���߶�2+3����
������Ϊ4��4ʱ�����в�ͬ���߶�2+3+4����
��ô������Ϊ5��5ʱ�����в�ͬ���߶�2+3+4+5����
��2��������Ϊ��n-1������n-1��ʱ�����в�ͬ���߶�2+3+4+5+��+��n-1������������Ϊn��nʱ�����в�ͬ���߶�2+3+4+5+��+��n-1��+n��������ֲ�ͬ���ȵ��߶�����������n�֣�
��3��������Ϊn��nʱ�����в�ͬ���߶�Ӧ��2��ʼ�ӣ��ӵ�n��
���������(1)4��2+3+4+5(��14)
(2)��n��n�Ķ��Ӱ��(n-1)��(n-1)�Ķ��Ӱ��в�ͬ���ȵ��߶�����������n�ֻ�ڷֱ���a,b��ʾn��n��(n-1)��(n-1)�Ķ��Ӱ��в�ͬ���ȵ��߶�����,��a=b+n.
(3)S=2+3+4+��+n=![]() ��(n-1)=
��(n-1)= ![]() .
.

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�