题目内容
【题目】（1）分解因式：xy2﹣2xy+x
（2）若代数式﹣3x，
﹣1，1在数轴上位置为从左往右依次排列，求x的取值范围．
（3）化简：
（4）先化简，再求值
，其中x＝
．
【答案】（1）x（y﹣1）2；(2)
；(3)
；（4）
，-2.
【解析】
(1)先提取公因式x，再利用完全平方公式分解可得；
(2)根据左边的数小于右边的数列出关于x的不等式组，解之可得；
(3)先计算括号内的加法、除法转化为乘法，再计算乘法即可得；
(4)先根据分式混合运算顺序和运算法则化简原式，再将x的值代入计算可得．
解：（1）原式＝x（y2﹣2y+1）＝x（y﹣1）2；
（2）由题意，得：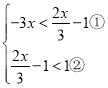
，
解不等式①，得：x＞
，
解不等式②，得：x＜3，
则；
（3）原式＝
＝
＝；
（4）原式＝
＝
＝
＝，
当x＝
时，
原式＝
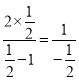＝﹣2．
练习册系列答案
阅读快车系列答案
相关题目
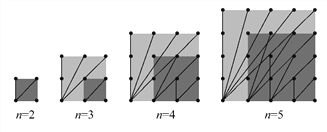
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
，所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, 
，2, 
，2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+（____） |
5×5 | （________） |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
