题目内容
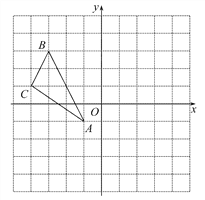
【题目】在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.(请利用网格作图,画出的线请用铅笔描粗描黑)

(1)过点C画AB的垂线,并标出垂线所过格点E;
(2)过点C画AB的平行线CF,并标出平行线所过格点F;
(3)直线CE与直线CF的位置关系是 ;
(4)连接AC,BC,则三角形ABC的面积为 .
【答案】(1)如图,直线CE即为所求;见解析;(2)如图,直线CF即为所求;见解析;(3)CE⊥CF(4)![]() .
.
【解析】
(1)构造全等三角形解决问题即可;
(2)构造平行四边形解决问题即可;
(3)根据平行线的性质即可判断;
(4)利用分割法计算三角形的面积即可;
解:(1)如图,直线CE即为所求;
(2)如图,直线CF即为所求;
(3)∵CF∥AB,CE⊥AB,
∴CE⊥CF;
(4)S△ABC=20﹣![]() ×3×4﹣
×3×4﹣![]() ×1×4﹣
×1×4﹣![]() ×1×5=
×1×5=![]() .
.


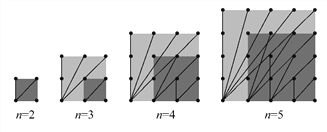
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
【题目】光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |

请根据以上提供的信息,解答下列问题:
(1)直接写出频数分布表中a,b,c的值,补全频数分布直方图.
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?