题目内容
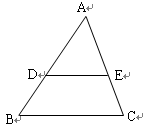
△ABC中,∠BAC=90°AD⊥BC于D,若AB=2,BC=3,则CD的长= 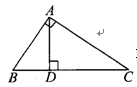

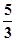
分析:由AD与BC垂直,根据垂直的定义得到∠ADB为90°,又∠BAC=90°,可得出两角相等,再由∠B为公共角,利用两对对应角相等的两三角形相似可得出三角形ABD与三角形CAB相似,根据相似得比例,将AB及BC的值代入求出BD的长,再由BC-BD即可求出CD的长.
解:∵AD⊥BC,∴∠ADB=90°,
又∠BAC=90°,
∴∠ADB=∠BAC,又∠B=∠B,
∴△ABD∽△CAB,
∴
 =
=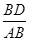 ,即AB2=BC?BD,
,即AB2=BC?BD,∵AB=2,BC=3,
∴BD=
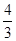 ,
,则CD=BC-BD=3-
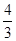 =
=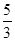 .
.故答案为:
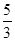

练习册系列答案
相关题目
 中,点
中,点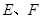 分别在边
分别在边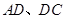 上,
上,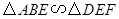
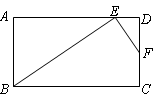 ,求
,求 的长
的长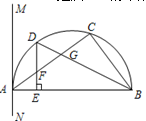
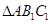 ,并写出点
,并写出点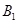 的坐标:
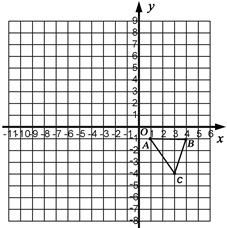
的坐标: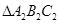 ,使得它与△ABC的位似比等于2:1 .
,使得它与△ABC的位似比等于2:1 .