��Ŀ����
����Ŀ���Ķ���С��������ķ�����![]() �Ľ⣮
�Ľ⣮
�ⷨ 1����![]() ����x=t2��ԭ���̻�Ϊt -3t2=0���ⷽ��t -3t2=0����t1=0��t2=
����x=t2��ԭ���̻�Ϊt -3t2=0���ⷽ��t -3t2=0����t1=0��t2=![]() ��
��
����![]() ��
��![]() ��������
��������![]() ��
��![]() ����ƽ������x=0��
����ƽ������x=0��![]() ��
��
�����飺x=0��![]() ����ԭ���̵Ľ⣬����ԭ���̵Ľ�Ϊx=0��
����ԭ���̵Ľ⣬����ԭ���̵Ľ�Ϊx=0��![]() ��
��
�ⷨ 2������� ![]() ����������ͬʱƽ������x=9x2���ⷽ��x=9x2����x=0��
����������ͬʱƽ������x=9x2���ⷽ��x=9x2����x=0��![]() ��
��
�����飺x=0��![]() ����ԭ���̵Ľ⣬����ԭ���̵Ľ�Ϊx=0��
����ԭ���̵Ľ⣬����ԭ���̵Ľ�Ϊx=0��![]() ��
��
��1������![]() �����ݶ���д����������
�����ݶ���д����������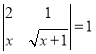 �ķ��̣�
�ķ��̣�
��2�������1����д���ķ��̵Ľ⣮
���𰸡���1��![]() ����2��x1=3��x2=-1
����2��x1=3��x2=-1
��������
��1�����ö���������㣬������Ӧλ�õ�����ʽ�Ӽ��ɵõ����̣�
��2��������Ŀ�и����ķ�������ѡ��һ�ⷽ�̼��ɣ�
��1����![]() ��
��
��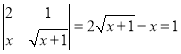 ��
��
��2�������![]() ��
��
��������ͬʱƽ������![]() ��
��
�����ã�![]() ��
��
���![]() ��
��
�����飬![]() ����ԭ���̵Ľ⣬
����ԭ���̵Ľ⣬
��ԭ���̵Ľ�Ϊ![]() ��
��

��ϰ��ϵ�д�
 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
�����Ŀ