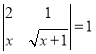Question

【题目】在△ABC中，AB＝AC＝5，sinB＝，⊙O过点B、C两点，且⊙O半径r＝，则OA的长为_____．

Answer 1

【答案】3或5

【解析】

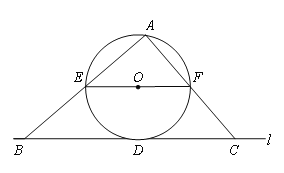
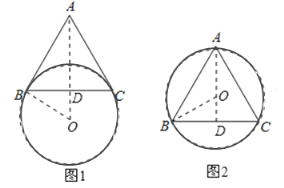
作AD⊥BC于D，由于AB＝AC＝5，根据等腰三角形的性质得AD垂直平分BC，根据垂径定理的推论得到点O在直线AD上，连结OB，在Rt△ABD中，根据正弦的定义计算出AD＝4，根据勾股定理计算出BD＝3，再在Rt△OBD中，根据勾股定理计算出OD＝1，然后分类讨论：①当点A与点O在BC的两侧，有OA＝AD+OD；②当点A与点O在BC的同侧，有OA＝AD﹣OD，即求得OA的长．

解：如图，作AD⊥BC于D，

∵AB＝AC＝5，

∴AD垂直平分BC，

∴点O在直线AD上，

连结OB，

在Rt△ABD中，sin∠ABD＝＝，

∵AB＝5，∴AD＝4，

∴BD＝＝＝3，

在Rt△OBD中，OB＝，BD＝3，

∴OD＝＝1，

当点A与点O在BC的两侧时，如图1，OA＝AD+OD＝4+1＝5；

当点A与点O在BC的同侧时，如图2，OA＝AD﹣OD＝4﹣1＝3，

故OA的长为3或5．

故答案为：3或5．