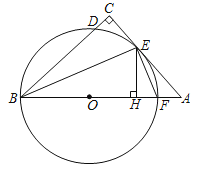
题目内容
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 将
将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连结
,连结![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 其中正确结论的序号是______.
其中正确结论的序号是______.
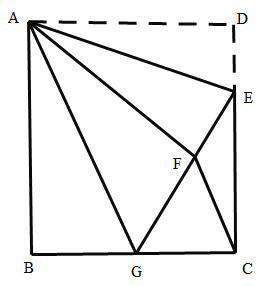
【答案】①②③
【解析】
由翻折的性质可得AF=AD,∠AFE=∠D=90°,DE=EF,由“HL”证明Rt△ABG≌Rt△AFG,得出①正确;由全等三角形对应边相等可得BG=FG,再求出DE的长,设BG=x,得出CG、EG,由勾股定理列出方程求出x,得出BG=FG=CG,得出②正确;由等边对等角可得∠GCF=∠GFC,由全等三角形对应角相等可得∠AGB=∠AGF,由三角形的外角性质得出∠BGF=∠GCF+∠GFC,得出∠AGB=∠GCF=∠GFC,得出③正确;然后求出△CEG的面积,再根据等高的三角形的面积的比等于底边的比求出△CEF的面积,得出④错误,即可求解.
解:∵△ADE沿AE对折至△AFE,
∴AF=AD,∠AFE=∠D=90°,DE=EF,
∵四边形ABCD是正方形,
∴AB=AD,
∴AB=AF,
在Rt△ABG和Rt△AFG中,
AB=AF,AG=AG,
∴Rt△ABG≌Rt△AFG(HL),故①正确;
∴BG=FG,
∵AB=6,CD=3DE,
∴DE=2,CE=62=4,
设BG=x,则CG=6x,EG=x+2,
在Rt△CEG中,CG2+CE2=EG2,
即(6x)2+42=(x+2)2,
解得:x=3,
∴BG=FG=CG=3,故②正确;
∴∠GCF=∠GFC,
由Rt△ABG≌Rt△AFG得,∠AGB=∠AGF,
由三角形的外角性质,∠BGF=∠GCF+∠GFC,
∴∠AGB=∠GCF=∠GFC,
故③正确;
∵EF=DE=2,FG=3,则GE=5,
∴S△CEF=![]() S△GCE,
S△GCE,
∵S△GCE=![]() ×GC×EC=6
×GC×EC=6
∴S△CEF=![]() ×6=
×6=![]() ,故④错误;
,故④错误;
故答案为:①②③.