题目内容
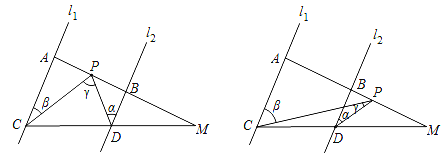
【题目】如图,已知l1∥l2,线段MA分别与直线l1,l2交于点A,B,线段MC分别与直线l1,l2交于点C,D,点P在线段AM上运动(P点与A,B,M三点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)若点P在A,B两点之间运动时,若a=25°,β=40°,那么γ= .
(2)若点P在A,B两点之间运动时,探究α,β,γ之间的数量关系,请说明理由;
(3)若点P在B,M两点之间运动时,α,β,γ之间有何数量关系?(只需直接写出结论)
【答案】(1)65°;(2)γ=α+β,理由见解析;(3)β﹣α=γ.
【解析】
(1)利用平行线的性质,三角形内角和定理即可证明.
(2)利用平行线的性质,三角形内角和定理即可证明.
(3)利用平行线的性质以及三角形的外角的性质即可解决问题.
(1)∵AC∥BD,
∴β+∠PCD+∠PDC+α=180°,
∵γ+∠PCD+∠PDC=180°,
∴γ=α+β=65°.
(2)∵AC∥BD,
∴β+∠PCD+∠PDC+α=180°,
∵γ+∠PCD+∠PDC=180°,
∴γ=α+β.
(3)如图,当P在B,M之间时,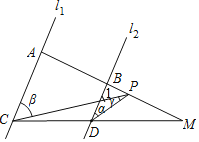
∵AC∥BD,
∴∠1=β,
∵∠1=α+γ,
∴β=α+γ.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】小明同学以“你最喜欢的运动项目”为主题,对公园里参加运动的群众进行随机调查(每名被调查者只能选一个项目,且被调查者都进行了选择).下面是小明根据调查结果列出的统计表和绘制的扇形统计图(不完整).
被调查者男、女所选项目人数统计表
项目 | 男(人数) | 女(人数) |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|

根据以上信息回答下列问题:
(1)统计表中的![]() __________,
__________,![]() __________.
__________.
(2)扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
(3)若平均每天来该公园运动的人数有3600人,请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人?