题目内容
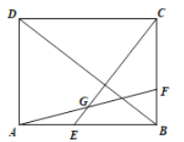
【题目】如图,在矩形![]() 中,
中,![]() 为对角线,过点
为对角线,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则线段
,则线段![]() 的长为______.
的长为______.
【答案】![]()
【解析】
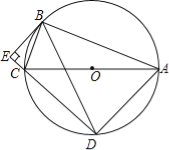
连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.利用全等三角形的性质证明OC=CM,∠ACG=∠GCM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,可得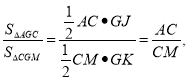
 推出AG=2GM,证明△MOG≌△MBF(AAS),可得OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,利用勾股定理构建方程组即可解决问题.
推出AG=2GM,证明△MOG≌△MBF(AAS),可得OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,利用勾股定理构建方程组即可解决问题.
解:连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.

∵四边形ABCD是矩形, ∴OA=OC,
∵AG=GF=CF, ∴∠FCG=∠FGC,OG∥CF,
∴∠OGC=∠FCG=∠FGC,
∵CE⊥BD, ∴∠GNO=∠GNM=90°,
∵GN=GN, ∴△GNO≌△GNM(ASA),
∴ON=NM,OG=GM,
∵∠CNO=∠CNM=90°,CN=CN,
∴△CNO≌△CNM(SAS),
∴∠OCN=∠MCN,OC=MC= ![]() AC,
AC,
∴GC平分∠ACM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,
∴ 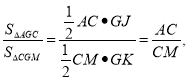
同理:
![]()
∴AG=2GM,
∵AG=GF, ∴GM=MF,
∵∠MOG=∠MBF,∠OMG=∠BMF,
∴△MOG≌△MBF(AAS),
∴OG=BF=GM=FM,
设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,
∴BC=3k,
在Rt△ABF中,∵![]() ∴
∴![]() ①,
①,
在Rt△ABC中,∵![]() AC=BD=
AC=BD= ![]()
∴![]() ②,
②,
由①②可得AB=![]()
故答案为![]()

练习册系列答案
相关题目