题目内容
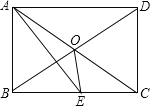
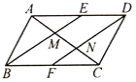
【题目】如图，在平行四边形ABCD中E、F分别是边AD、BC的中点，AC分别交BE、DF于点M、N，对于下列结论：①△ABE≌△CDF；②AM=MN=NC；③EM=
BM，④S△ABM=S△AME，其中正确的有（ ）
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①已知四边形ABCD是平行四边形，可得AB=CD，AD=BC，∠DAB=∠DCB，已知E、F分别是边AD、BC的中点，可得AE=
AD=CF=BC，可证得△ABE≌△CDF
②证明△ABM≌△CDN，得到AM=CN，再证明BE∥DF，F分别是边BC的中点，可得CN=MN，即可得出AM=CN=MN
③证明ME=ND，因为△ABM≌△CDN，可得BM=DN，ME=BM，可判断③
④在求△ABM和△AME面积时，有同一个高，它们的底分别为BM，ME，比较底边大小即可求解．
①∵四边形ABCD是平行四边形
∴AB=CD，AD=BC，∠DAB=∠DCB
∵E、F分别是边AD、BC的中点
∴AE=AD=CF=BC
∴△ABE≌△CDF
故①正确
②∵△ABE≌△CDF
∴∠ABM=∠NDC
∵四边形ABCD是平行四边形，AB∥CD
∴∠BAM=∠NCD，AB=CD
∴△ABM≌△CDN
∴AM=CN，
∵∠AEB=∠DFC
∵AD∥BC
∴∠AEB=∠EBC
∴∠DFC=∠EBC
∴BE∥DF
∵F是边BC的中点
∴CN=MN
即AM=CN=MN
故②正确
③∵BE∥DF，E是边AD的中点
∴M是边AN的中点，即ME是△AND的中位线
∴ME=ND
∵△ABM≌△CDN
∴BM=DN
∴ME=BM
故③正确
④过点A作AH⊥BE于H，如图所示
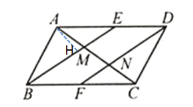
在求△ABM和△AME面积时，有同一个高AH，它们的底分别为BM，ME，
∵EM=BM ，
∴S△ABM＞S△AME
故④错误
综上所述①②③正确
故选：C
期末冲刺100分创新金卷完全试卷系列答案
