题目内容
【题目】已知,点E在正方形![]() 的
的![]() 边上(不与点B,C重合),
边上(不与点B,C重合),![]() 是对角线,延长
是对角线,延长![]() 到点F,使
到点F,使![]() ,过点E作
,过点E作![]() 的垂线,垂足为G,连接
的垂线,垂足为G,连接![]() ,
,![]() .
.

(1)根据题意补全图形,并证明![]() ;
;
(2)①用等式表示线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)补全图形后,如下图所示,证明△EGC为等腰三角形即可;
(2)①连接GF,GD,证明△BGE≌△FGC,得到GF=GB,再证明△ABG≌△ADG,得到GD=GF,进一步得到△DGF为等腰直角三角形,进而得到![]() ;
;
②连接AE,证明△ABE≌△DCF,得到DF=AE,在Rt△AEG中由勾股定理得到![]() ,进而得到
,进而得到![]() .
.
解:(1)补全图形如下所示:
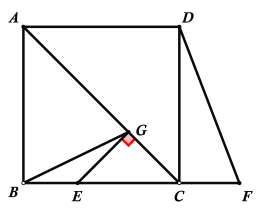
证明:∵四边形ABCD为正方形,AC是对角线
∴∠GCE=45°
∵EG⊥AC
∴∠EGC=90°
∴∠GEC=∠GCE=45°
∴△GEC为等腰直角三角形
∴GC=GE.
(2)①连接GF,GD,如下图所示:
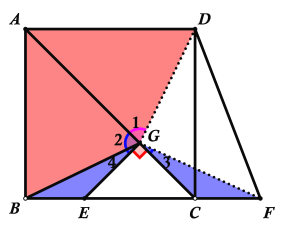
由(1)知:∠GEB=180°-∠GEC=180°-45°=135°,∠GCF=180°-∠GCE=180°-45°=135°
∴∠GEB=∠GCF
在△GBE和△GCF中
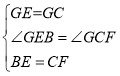 ,∴△GBE≌△GCF(SAS)
,∴△GBE≌△GCF(SAS)
∴GF=GB,且∠3=∠4
在△ABG和△ADG中
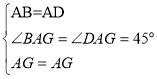 ,∴△ABG≌△ADG(SAS)
,∴△ABG≌△ADG(SAS)
∴GB=GD,∠1=∠2
故GF=GD,△GDF为等腰三角形
又∠2+∠4=90°
∴∠1+∠3=90°,即∠DGF=90°
∴△GDF为等腰直角三角形
∴![]() .
.
故答案为:![]() .
.
②连接AE,如下图所示:
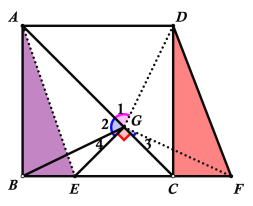
在△ABE和△DCF中
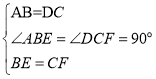 ,∴△ABE≌△DCF(SAS)
,∴△ABE≌△DCF(SAS)
∴![]()
又由①中知:![]()
∴![]()
且![]()
在Rt△AGE中,由勾股定理:![]() ,将上述等式代入:
,将上述等式代入:
故有![]()
即:![]() .
.
故线段![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]() .
.
故答案为:![]() .
.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目