题目内容
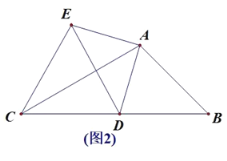
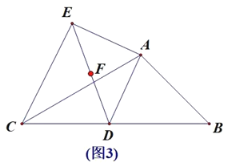
【题目】边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 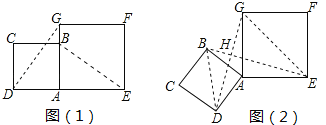
【答案】6
【解析】试题分析:)∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,AG=AE,∠DAB=∠EAG=90°,
∴∠DAB+∠BAG =∠EAG+∠BAG,
∴∠DAG=∠BAE,
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,
在正方形AEFG中,∠AGE=∠AEG=45°,
∴∠HGE+∠HEG=45°+∠AGD+45°-∠AEB=90°,
所以∠GHE=90°,
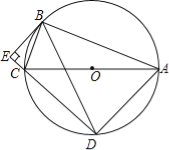
所以对于△EGH,点H在以EG为直径的圆上,
∴当点H与点A重合时,△EGH的高最大;
同理对于△BDH,点H在以BD为直径的圆上,
∴当点H与点A重合时,△BDH的高最大,
∴△GHE和△BHD面积之和的最大值为: ![]() ×22+
×22+![]() ×(2
×(2![]() )2=2+4=6.
)2=2+4=6.
故答案为6.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
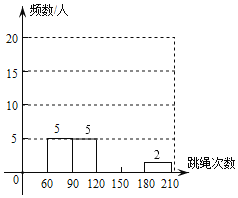
【题目】学校为了了解七年学生跳绳情况,从七年级学生中随机抽查了50名学生进行1分钟跳绳测试,并对测试结果统计后绘制了如下不完整统计图表,请根据图表中的信息解答下列问题.
组别 | 次数 | 频数(人) | 百分比 |
1 | 60≤x<90 | 5 | 10% |
2 | 90≤x<120 | 5 | b |
3 | 120≤x<150 | 18 | 36% |
4 | 150≤x<180 | a | c |
5 | 180≤x<210 | 2 | 4% |
合计 | 50 | 1 | |
(1)直接写出a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生400人,请你估计该校七年级学生跳绳次数在90≤x<150范围的学生约有多少人?(