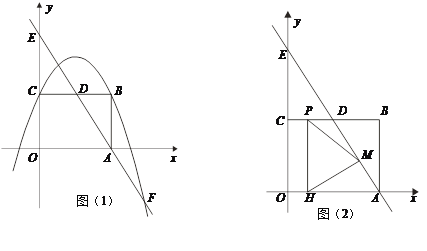Question

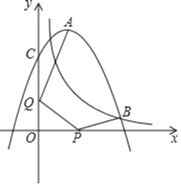
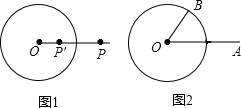
【题目】我们定义：如果圆的两条弦互相垂直，那么这两条弦互为“十字弦”，也把其中的一条弦叫做另一条弦的“十字弦”.如：如图，已知的两条弦，则、互为“十字弦”，是的“十字弦”，也是的“十字弦”.

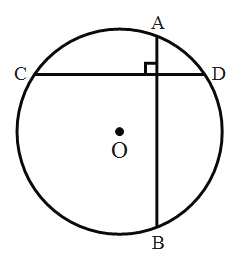
（1）若的半径为5，一条弦，则弦的“十字弦”的最大值为______，最小值为______.

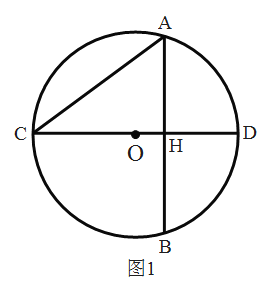
（2）如图1，若的弦恰好是的直径，弦与相交于，连接，若，，，求证：、互为“十字弦”；

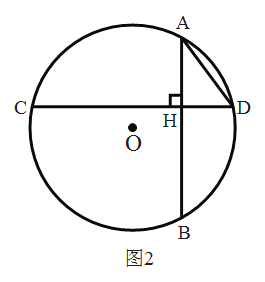
（3）如图2，若的半径为5，一条弦，弦是的“十字弦”，连接，若，求弦的长.

Answer 1

【答案】（1）10，6；（2）见解析；（3）.

【解析】

（1）根据“十字弦”定义可得弦的“十字弦”为直径时最大，当CD过A点或B点时最小；

（2）根据线段长度得出对应边成比例且有夹角相等，证明△ACH∽△DCA,由其性质得出对应角相等，结合90°的圆周角证出AH⊥CD，根据“十字弦”定义可得；

（3）过O作OE⊥AB于点E，作OF⊥CD于点F,利用垂径定理得出OE=3，由正切函数得出AH=DH,设DH=x，在Rt△ODF中，利用线段和差将边长用x表示，根据勾股定理列方程求解.

解：（1）当CD为直径时，CD最大，此时CD=10，

∴弦的“十字弦”的最大值为10；

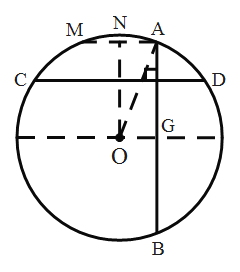
当CD过A点时，CD长最小，即AM的长度,过O点作ON⊥AM,垂足为N,作OG⊥AB，垂足为G,则四边形AGON为矩形，

∴AN=OG,

∵OG⊥AB,AB=8，

∴AG=4，

∵OA=5，

∴由勾股定理得OG=3，

∴AN=3，

∵ON⊥AM,

∴AM=6，

即弦的“十字弦”的最小值是6.

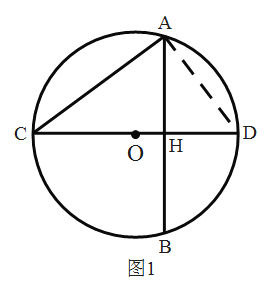
（2）证明：如图，连接AD，

∵，，，

∴ ,

∵∠C=∠C,

∴△ACH∽△DCA,

∴∠CAH=∠D,

∵CD是直径，

∴∠CAD=90°,

∴∠C+∠D=90°,

∴∠C+∠CAH=90°,

∴∠AHC=90°,

∴AH⊥CD,

∴、互为“十字弦”.

（3）如图，过O作OE⊥AB于点E，作OF⊥CD于点F，连接OA，OD，则四边形OEHF是矩形，∴OE=FH,OF=EH,

∴AE=4，

∴由勾股定理得OE=3，

∴FH=3，

∵tan∠ADH=,

∴tan60°= ,

设DH=,则AH=x,

∴FD=3+x,OF=HE=4 -x,

在Rt△ODF中，由勾股定理得，OD2=OF2+FD2，

∴(3+x)2+(4 -x)2=52,

解得，x= ,

∴FD=,

∵OF⊥CD,

∴CD=2DF=

即CD=