Question

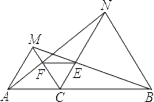
【题目】如图，已知C为线段AB上的一点，△ACM和△CBN都是等边三角形，AN和CM相交于F点，BM和CN交于E点．求证：△CEF是等边三角形．

Answer 1

【答案】见解析

【解析】

由等边三角形的性质可得AC=CM，BC=CN，再利用角的和差可得到∠ACN=∠MCB，可证明△ACN≌△MCB，可得∠ENC=∠FBC，由条件可得∠ECF=60°，可证明△CEN≌△CFB，可得CE=CF，可知△CEF为等边三角形．

证明：∵△ACM和△CBN是等边三角形，

∴AC＝MC，BC＝CN，∠MCA＝∠NCB＝60°，

∴∠ACN＝∠MCB＝120°，

在△ACN和△MCB中，

，

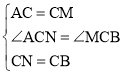∴△ACN≌△MCB（SAS），

∴∠ANC＝∠MBC，

∵△ACM和△CBN是等边三角形，

∴∠MCA＝∠NCB＝60°，

∴∠ECF＝180°﹣60°﹣60°＝60°，

在△CFN和△CEB中，

，

∴△CFN≌△CEB（ASA），

∴CE＝CF，

∵∠ECF＝60°，

∴△CEF为等边三角形．