题目内容
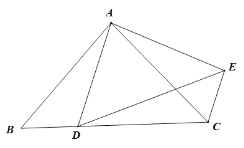
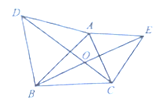
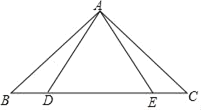
【题目】如图,在△ABC中,∠B=∠C=40°,点D、点E分别从点B、点C同时出发,在线段BC上作等速运动,到达C点、B点后运动停止.
(1)求证:△ABE≌△ACD;
(2)若AB=BE,求∠DAE的度数;
拓展:若△ABD的外心在其内部时,求∠BDA的取值范围.
【答案】(1)证明见解析;(2)![]() ;拓展:
;拓展:![]()
【解析】
(1)由题意得BD=CE,得出BE=CD,证出AB=AC,由SAS证明△ABE≌△ACD即可;
(2)由等腰三角形的性质和三角形内角和定理求出∠BEA=∠EAB=70°,证出AC=CD,由等腰三角形的性质得出∠ADC=∠DAC=70°,即可得出∠DAE的度数;
拓展:对△ABD的外心位置进行推理,即可得出结论.
(1)证明:∵点D、点E分别从点B、点C同时出发,在线段BC上作等速运动,
∴BD=CE,
∴BC-BD=BC-CE,即BE=CD,
∵∠B=∠C=40°,
∴AB=AC,
在△ABE和△ACD中,
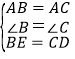 ,
,
∴△ABE≌△ACD(SAS);
(2)解:∵∠B=∠C=40°,AB=BE,
∴∠BEA=∠EAB=![]() (180°-40°)=70°,
(180°-40°)=70°,
∵BE=CD,AB=AC,
∴AC=CD,
∴∠ADC=∠DAC=![]() (180°-40°)=70°,
(180°-40°)=70°,
∴∠DAE=180°-∠ADC-∠BEA=180°-70°-70°=40°;
拓展:
解:若△ABD的外心在其内部时,则△ABD是锐角三角形.
∴∠BAD=140°-∠BDA<90°.
∴∠BDA>50°,
又∵∠BDA<90°,
∴50°<∠BDA<90°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目