Question

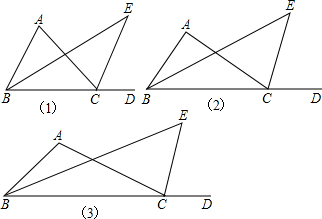
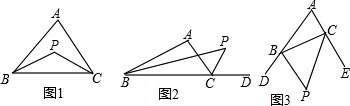
（1）如图1，△ABC中，∠ABC与∠ACB的平分线交与点P，求证：∠P=90°+

1

2

∠A．
（2）如图2，在上题中，如果CP是∠ACD的平分线，BP是∠ABC的平分线，那么∠P与∠A有什么关系？并证明你的结论．
（3）如图3在上题中，如果BP、CP分别是∠CBD与∠BCE的平分线，那么∠P与∠A有什么关系？直接写出关系，不必证明．

Answer 1

（1）证明：∵∠ABC与∠ACB的平分线交与点P，
∴∠PBC+∠PCB=

1

2

（∠ABC+∠ACB），
∵∠ABC+∠ACB=180°-∠A，
∴∠P=180°-

1

2

（∠ABC+∠ACB）=180°-

1

2

（180°-∠A）=90°+

1

2

∠A；

（2）证明：∵BP、CP分别为∠ABC、∠ACD的平分线，
∴∠PBC=

1

2

∠ABC，∠PCD=

1

2

∠ACD，
根据三角形的外角性质，∠ACD=∠A+∠ABC，
∠PCD=∠PBC+∠P，
∴∠BAC+∠ABC=2（∠PBC+∠P）=2∠PBC+2∠P，
∴∠BAC=2∠P，
∴∠P=

1

2

∠BAC，即∠P=

1

2

∠A；

（3）BP、CP为△ABC两外角∠ABC、∠ACB的平分线，∠A为x°
∴∠BCP=

1

2

（∠A+∠ABC）、∠PBC=

1

2

（∠A+∠ACB），
由三角形内角和定理得，∠BPC=180°-∠BCP-∠PBC，
=180°-

1

2

[∠A+（∠A+∠ABC+∠ACB）]，
=180°-

1

2

（∠A+180°），
=90°-

1

2

∠A，即∠P=90°-

1

2

∠A．