题目内容
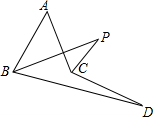
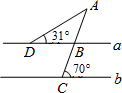
如图所示，在△ABC中，∠ACB为直角，∠CAD的角平分线交BC的延长线于点E，若∠B=35°，求∠BAE和∠E的度数．
∵△ABC中，∠ACB为直角，∠B=35°，
∴∠BAC=180°-90°-35°=55°，
∴∠CAD=180°-∠BAC=180°-55°=125°，
∵AE是∠CAD的平分线，
∴∠CAE=
∠CAD=
×125°=62.5°，
∴∠BAE=∠BAC+∠CAE=55°+62.5°=117.5°，∠E=90°-∠CAE=90°-62.5°=27.5°．
∴∠BAC=180°-90°-35°=55°，
∴∠CAD=180°-∠BAC=180°-55°=125°，
∵AE是∠CAD的平分线，
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BAE=∠BAC+∠CAE=55°+62.5°=117.5°，∠E=90°-∠CAE=90°-62.5°=27.5°．
练习册系列答案
阅读快车系列答案
相关题目
