Question

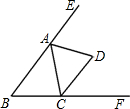
如图，在△ABC中，∠ABC、∠ACB的平分线相交于点D，∠BDC=120°，则∠A=______．

Answer 1

∵在△BCD中，∠DBC+∠DCB+∠BDC=180°
∴∠DBC+∠DCB=180°-120°=60°．
∵BD和CD是∠ABC，∠ACB的角平分线，
∴∠DBC=

1

2

∠ABC，∠DCB=

1

2

∠ACB
∴∠DBC+∠DCB=

1

2

（∠ABC+∠ACB）
∴∠ABC+∠ACB=2（∠DBC+∠DCB）=2×60°=120°．
又∵△ABC中，∠ABC+∠ACB+∠A=180°，
∴∠A=180°-（∠ABC+∠ACB）=180°-120°=60°．
故答案是：60°．