题目内容
【题目】如图,二次函数y= ![]() x2+bx﹣
x2+bx﹣ ![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标:;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
【答案】
(1)(﹣3,4)
(2)
解:设PA=t,OE=l
由∠DAP=∠POE=∠DPE=90°得△DAP∽△POE
∴ ![]()
∴l=﹣ ![]() +
+ ![]() =﹣
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]()
∴当t= ![]() 时,l有最大值
时,l有最大值 ![]()
即P为AO中点时,OE的最大值为 ![]()
(3)
解:存在.
①点P点在y轴左侧时,DE交AB于点G,
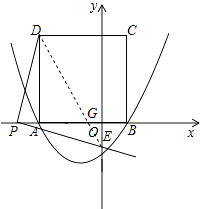
P点的坐标为(﹣4,0),
∴PA=OP﹣AO=4﹣3=1,
由△PAD≌△EOP得OE=PA=1
∵△ADG∽△OEG
∴AG:GO=AD:OE=4:1
∴AG= ![]() =
= ![]()
∴重叠部分的面积= ![]() =
= ![]()
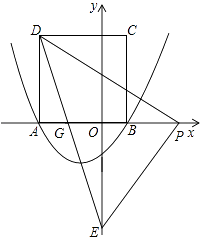
②当P点在y轴右侧时,P点的坐标为(4,0),
此时重叠部分的面积为 ![]()
【解析】解:(1)(﹣3,4);

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则 ①DE=DF;②DF=EF;③△DCF≌△DGE;④EF= ![]() .
.
上面结论正确的有( )
A.1个
B.2个
C.3个
D.4个
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.