题目内容
【题目】如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为C′,再将所折得的图形沿EF折叠,使得点D和点A重合.若AB=3,BC=4,则折痕EF的长为 
【答案】![]()
【解析】解: 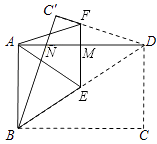
设BC′与AD交于N,EF与AD交于M,
根据折叠的性质可得:∠NBD=∠CBD,AM=DM= ![]() AD,∠FMD=∠EMD=90°,
AD,∠FMD=∠EMD=90°,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=4,∠BAD=90°,
∴∠ADB=∠CBD,
∴∠NBD=∠ADB,
∴BN=DN,
设AN=x,则BN=DN=4﹣x,
∵在Rt△ABN中,AB2+AN2=BN2 ,
∴32+x2=(4﹣x)2 ,
∴x= ![]() ,
,
即AN= ![]() ,
,
∵C′D=CD=AB=3,∠BAD=∠C′=90°,∠ANB=∠C′ND,
∴△ANB≌△C′ND(AAS),
∴∠FDM=∠ABN,
∴tan∠FDM=tan∠ABN,
∴ ![]() ,
,
∴ ![]() ,
,
∴MF= ![]() ,
,
由折叠的性质可得:EF⊥AD,
∴EF∥AB,
∵AM=DM,
∴ME= ![]() AB=
AB= ![]() ,
,
∴EF=ME+MF= ![]() +
+ ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

【题目】如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则 ①DE=DF;②DF=EF;③△DCF≌△DGE;④EF= ![]() .
.
上面结论正确的有( )
A.1个
B.2个
C.3个
D.4个
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
【题目】小明用下面的方法求出方程2 ![]() ﹣3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
﹣3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
2 | 令 | t= | t= |
|
x﹣2 | ||||
x+2+ |




