Question

【题目】函数y＝x2﹣4x+3

（1）求其图象与x轴交点A、B的坐标（A在B左边）；

（2）在坐标系中画出函数图象；

（3）若函数图形的顶点为C，求△ABC的面积．

Answer 1

【答案】（1）点A的坐标为（1，0），点B的坐标为（3，0）；（2）详见解析；（3）1

【解析】

（1）根据题目中的函数解析式可以求得点A和点B的坐标；

（2）根据函数解析式可以求得该函数的顶点坐标，从而可以画出相应的函数图象；

（3）根据点A、B、C的坐标可以求得△ABC的面积．

解：（1）∵y＝x2﹣4x+3＝（x﹣1）（x﹣3），

∴当y＝0时，x1＝1，x2＝3，

∴点A的坐标为（1，0），点B的坐标为（3，0）；

（2）∵y＝x2﹣4x+3＝（x﹣2）2﹣1，

∴该抛物线的顶点坐标为（2，﹣1），

该函数的图象有右图所示；

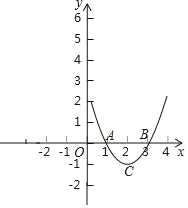
（3）由（2）知顶点C的坐标为（2，﹣1），

∵点A的坐标为（1，0），点B的坐标为（3，0），

∴AB＝2，

∴△ABC的面积是：AB×h=＝1．