题目内容
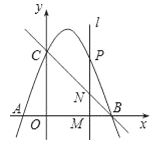
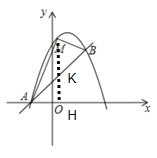
【题目】如图,已知直线AB与抛物线C:y=ax2+2x+c相交于点A(﹣1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式;
(2)若点M是位于直线AB上方抛物线上的一动点,当![]() 的面积最大时,求此时
的面积最大时,求此时![]() 的面积S及点M的坐标.
的面积S及点M的坐标.

【答案】(1) y=﹣x2+2x+3;(2) △MAB的面积最大值是![]() ,M(
,M(![]() ,
,![]() )
)
【解析】
(1)利用待定系数法求出抛物线的解析式即可;
(2)过点M作MH⊥x轴于H,交直线AB于K,利用待定系数法可得yAB=x+1,设点M(x,﹣x2+2x+3),则K(x,x+1),可得S△MAB=![]() ,即可求出
,即可求出![]() 的最大面积S及点M的坐标.
的最大面积S及点M的坐标.
(1)由题意把点(﹣1,0)、(2,3)代入y=ax2+2x+c,
得![]() ,解得
,解得![]() ,
,
∴此抛物线C函数表达式为:y=﹣x2+2x+3;
(2)如图,过点M作MH⊥x轴于H,交直线AB于K,
将点(﹣1,0)、(2,3)代入y=kx+b中,
得![]() ,解得
,解得![]() ,
,
∴yAB=x+1,
设点M(x,﹣x2+2x+3),则K(x,x+1),则MK=﹣x2+2x+3﹣(x+1)=﹣x2+x+2,
∴S△MAB
=S△AMK+S△BMK
=![]() MK(xM﹣xA)+
MK(xM﹣xA)+ ![]() MK(xB﹣xM)
MK(xB﹣xM)
=![]() MK(xB﹣xA)
MK(xB﹣xA)
=![]() ×(-x2+x+2)×3
×(-x2+x+2)×3
=![]() ,
,
∵![]() ,当x=
,当x=![]() 时,S△MAB最大=
时,S△MAB最大=![]() ,此时
,此时![]() ,
,
∴△MAB的面积最大值是![]() ,M(
,M(![]() ,
,![]() ).
).

练习册系列答案
相关题目