题目内容
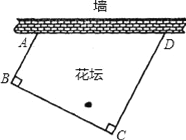
【题目】小区要用篱笆围成一个四边形花坛、花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米.围成的花坛是如图所示的四边形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围).
(2)当x是多少时,四边形ABCD面积S最大?最大面积是多少?
【答案】(1)S=﹣2x2+18x;(2)![]()
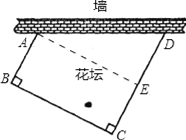
【解析】试题分析:(1)过点A作AE⊥CD于E,把四边形的面积分割为矩形ABCE和直角三角形AED的面积和即可;
(2)由(1)可知S和x为二次函数关系,根据二次函数的性质求其最大值即可.
试题解析:(1)过点A作AE⊥CD于E,
则∠AEC=∠AED=90°,
∵∠ABC=∠BCD=90°,
∴四边形ABCE是矩形,
∵BC=2AB.AB边的长为x米,
∴BC=2x,
∵四边形ABCE是矩形,
∴AB=CE=x,BC=AE=2x,
∵三边所用的篱笆之和恰好为18米,
∴CD=18﹣AB﹣BC=18﹣3x,
∴S四边形ABCD=S矩形ABCE+S△ADE=x2x+![]() DEAE=2x2+
DEAE=2x2+![]() (CD﹣CE)AE=﹣2x2+18x;
(CD﹣CE)AE=﹣2x2+18x;
(2)∵S=﹣2x2+18x;
a=﹣2<0,
∴S有最大值,
当x=﹣![]() =﹣
=﹣![]() =
=![]() 时,
时,
S最大=![]() =
=![]() .
.

练习册系列答案
相关题目