题目内容
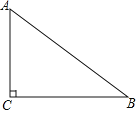
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的外心和内心之间的距离为_____.
【答案】![]()
【解析】
作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.先根据勾股定理求出AB=10,得到△ABC的外接圆半径AO=5,再证明四边形MECD是正方形,根据内心的性质和切线长定理,求出⊙M的半径r=2,则ON=1,然后在Rt△OMN中,运用勾股定理即可求解.
解:设△ABC的内切圆⊙M,O为△ACB的外接圆的圆心,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N,
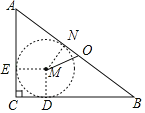
在Rt△ABC中,∵∠ACB=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
∵点O为△ABC的外心,
∴AO为外接圆半径,AO=![]() AB=5,
AB=5,
设⊙M的半径为r,则MD=ME=r,
又∵∠MDC=∠MEC=∠C=90°,
∴四边形IECD是正方形,
∴CE=CD=r,AE=AN=6﹣r,BD=BN=8﹣r,
∵AB=10,
解得:r=2,
∴MN=r=2,AN=AE=6﹣r=6﹣2=4,
在Rt△OMN中,∵∠MNO=90°,ON=AO﹣AN=5﹣4=1,
∴OM=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目