ЬтФПФкШн
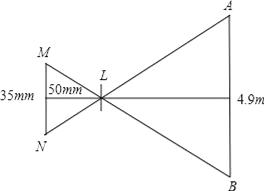
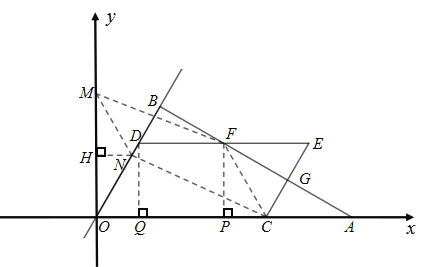
ЁОЬтФПЁПШчЭМЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAдкXжсЕФе§АыжсЃЌOA=8 ,ЕуBдкЕквЛЯѓЯоЃЌЁЯAOB=60ЁуЃЌABЁЭOBДЙзуЮЊB, ЕуDЁЂCЗжБ№дкБпOBЁЂOAЩЯЃЌЧвOD=AC=t,вдODЁЂOCЮЊБпзїЦНааЫФБпаЮOCED,DEНЛжБЯпABЮЊF,CEНЛжБЯпABЮЊЕуG.
(1) ЕБt=2ЪБЃЌ дђEЕФзјБъЮЊЁЁ ЁЁ
(2) ШєІЄDFCЕФУцЛ§ЮЊ![]() ЃЌЧѓtЕФжЕЁЃ
ЃЌЧѓtЕФжЕЁЃ
(3) ЕБDЁЂ B ЁЂGЁЂ EЫФЕуЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЪБЃЌдкYжсЩЯДцдкЕуM,Й§ЕуMзїFCЕФЦНааЯпНЛжБЯпOBЮЊЕуNЃЌШєвдMЁЂ NЁЂ FЁЂ CЮЊЖЅЕуЕФЫФБпаЮвВЪЧЦНааЫФБпаЮЃЌдђЕуMЕФзјБъЮЊ ЁЁ ЃЈжБНгаДГіД№АИЃЉ
ЁОД№АИЁПЃЈ1ЃЉ(7ЃЌ![]() )ЃЛЃЈ2ЃЉ
)ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЃЈ0ЃЌ
ЃЛЃЈ3ЃЉЃЈ0ЃЌ![]() ЃЉЃЌЃЈ0ЃЌ
ЃЉЃЌЃЈ0ЃЌ![]() ЃЉ.
ЃЉ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНааЫФБпаЮЕФаджЪвдМАЙДЙЩЖЈРэМЦЫуМДПЩЃЛ
ЃЈ2ЃЉИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌгУКЌtЕФДњЪ§ЪНЗжБ№БэЪОГіШ§НЧаЮЕФЕзКЭИпЃЌСаГіЗНГЬМДПЩЃЛ
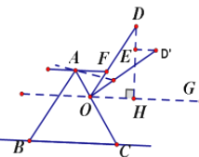
ЃЈ3ЃЉЯШИљОнЫФБпаЮBDGEЪЧЦНааЫФБпаЮМЦЫуГіtЕФжЕЃЛдйИљОнЫФБпаЮMNCFЪЧЦНааЫФБпаЮЫуГіЕуMЕФзјБъМДПЩЃЎ
ЃЈ1ЃЉЙ§ЕуDзїDQЁЭOAгкЕуQЃЌдђЁЯ DQO=90Ёу
ЕБt=2ЪБЃЌOD=AC=2
дђOC=OA-AC=8-2=6
дкЦНааЫФБпаЮOCEDжаЃЌDE=OC=6
дкRtЁїOQDжаЃЌЁЯAOB=60ЁуЃЌЁЯ DQO=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ![]()
ЁрЕуEЕФКсзјБъЮЊЃК1+6=7ЃЌзнзјБъЮЊЃК![]()
ЙЪЕуEЕФзјБъЮЊЃКЃЈ7ЃЌ![]() ЃЉ
ЃЉ
ЃЈ2ЃЉдкЦНааЫФБпаЮOCEDжаЃЌCE=OD=tЃЌЧвODЁЮCEЃЌOCЁЮDE
ЁпABЁЭOB
ЁрЁЯ ABO=90Ёу
гжЁпODЁЮCE
ЁрЁЯ AGC=90ЁуЃЌЁЯACG=ЁЯAOB=60ЁуЃЌ
дкRtЁїACGжаЃЌЁЯACG =60ЁуЃЌЁЯAGC =90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЁрCG=EG
ЁпOCЁЮDE
ЁрЁЯACG=ЁЯFEG
дкЁїACGКЭЁїFEGжаЃЌ
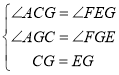
ЁрЁїACGЁеЁїFEG
ЁрEF=AC=t
Ёр![]()
гЩЃЈ1ЃЉжЊЃЌ![]() ЃЌдђ
ЃЌдђ![]()
Ёр![]()
гжЁпІЄDFCЕФУцЛ§ЮЊ![]()
Ёр![]()
НтЕУЃК![]() ЃЌ
ЃЌ![]()
ЃЈ3ЃЉЕБЕуMдкyжсе§АыжсЩЯЪБЃЛ
дкRtЁїAOBжаЃЌЁЯAOB =60ЁуЃЌЁЯABO =90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЁпЫФБпаЮBDGEЪЧЦНааЫФБпаЮ
Ёр![]()
Ёр![]()
гЩЃЈ2ЃЉжЊ![]()
Ёр![]()
НтЕУЃК![]()
Ёр![]()
ЁпOCЁЮDEЃЌDQЁЭOCЃЌFPЁЭOC
Ёр![]()
ШєЫФБпаЮMNCFЪЧЦНааЫФБпаЮЃЌ
дђгаMN=CF
гаЬтЩшЬѕМўвзЕУЃЌЁїCPFЁеЁїNHM
Ёр![]() ЃЌ
ЃЌ![]()
дкRtЁїOHNжаЃЌЁЯOHN =90ЁуЃЌЁЯHON =90Ёу-60Ёу=30ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЁрЕуMЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉ
ЃЉ
ЕБЕуMдкyжсИКАыжсЩЯЪБЃЛЭЌРэПЩЕУЕуMЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉ
ЃЉ
злЩЯЫљЪіЃКЕуMЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЛђЃЈ0ЃЌ
ЃЉЛђЃЈ0ЃЌ![]() ЃЉ
ЃЉ

ЁОЬтФПЁПЮЪЬтГЪЯжЃКЮвУЧжЊЕРЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЪЧЫЋЧњЯпЃЌФЧУДКЏЪ§yЃН
ЃЈxЃО0ЃЉЕФЭМЯѓЪЧЫЋЧњЯпЃЌФЧУДКЏЪ§yЃН![]() +nЃЈkЁЂmЁЂnЮЊГЃЪ§ЧвkЁй0ЃЉЕФЭМЯѓЛЙЪЧЫЋЧњЯпТ№ЃПЫќгыЗДБШР§КЏЪ§yЃН
+nЃЈkЁЂmЁЂnЮЊГЃЪ§ЧвkЁй0ЃЉЕФЭМЯѓЛЙЪЧЫЋЧњЯпТ№ЃПЫќгыЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓгадѕбљЕФЙиЯЕФиЃПШУЮвУЧвЛЦ№ПЊЦєЬНЫїжЎТУЁЁ
ЃЈxЃО0ЃЉЕФЭМЯѓгадѕбљЕФЙиЯЕФиЃПШУЮвУЧвЛЦ№ПЊЦєЬНЫїжЎТУЁЁ
ЬНЫїЫМПМЃКЮвУЧПЩвдНшМјвдЧАбаОПКЏЪ§ЕФЗНЗЈЃЌЪзЯШЬНЫїКЏЪ§yЃН![]() ЕФЭМЯѓЃЎ
ЕФЭМЯѓЃЎ
ЃЈ1ЃЉЬюаДЯТБэЃЌВЂЛГіКЏЪ§yЃН![]() ЕФЭМЯѓЃЎ
ЕФЭМЯѓЃЎ
ЂйСаБэЃК
x | Ё | Љ5 | Љ3 | Љ2 | 0 | 1 | 3 | Ё |
y | Ё | Ё |
ЂкУшЕуВЂСЌЯпЃЎ
ЃЈ2ЃЉЙлВьЭМЯѓЃЌаДГіИУКЏЪ§ЭМЯѓЕФСНЬѕВЛЭЌРраЭЕФЬиеїЃК
ЂйЁЁ ЁЁЂкЁЁ ЁЁЃЛ
РэНтдЫгУЃККЏЪ§yЃН![]() ЕФЭМЯѓЪЧгЩКЏЪ§yЃН
ЕФЭМЯѓЪЧгЩКЏЪ§yЃН![]() ЕФЭМЯѓЯђЁЁ ЁЁЦНвЦЁЁ ЁЁИіЕЅЮЛЃЌЦфЖдГЦжааФЕФзјБъЮЊЁЁ ЁЁЃЎ
ЕФЭМЯѓЯђЁЁ ЁЁЦНвЦЁЁ ЁЁИіЕЅЮЛЃЌЦфЖдГЦжааФЕФзјБъЮЊЁЁ ЁЁЃЎ
СщЛюгІгУЃКИљОнЩЯЪіЛКЏЪ§ЭМЯѓЕФОбщЃЌЯывЛЯыКЏЪ§yЃН![]() +2ЕФЭМЯѓДѓжТЮЛжУЃЌВЂИљОнЭМЯѓжИГіЃЌЕБxТњзуЁЁ ЁЁЪБЃЌyЁн3ЃЎ
+2ЕФЭМЯѓДѓжТЮЛжУЃЌВЂИљОнЭМЯѓжИГіЃЌЕБxТњзуЁЁ ЁЁЪБЃЌyЁн3ЃЎ