Question

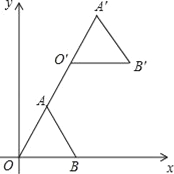
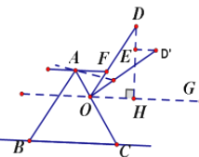
【题目】图 1 是小红在“淘宝双 11”活动中所购买的一张多档位可调节靠椅，档位调节示意图如图 2 所示。已知两支脚 AB=AC，O 为 AC 上固定连接点，靠背 OD=10 分米。档位为Ⅰ档时，OD∥AB，档位为Ⅱ挡时，OD’⊥AC,过点O作OG∥BC,则∠DOG+∠D’OG=_________°当靠椅由Ⅰ档调节为Ⅱ档时，靠背顶端 D 向后靠至 D’，此时点 D 移动的水平距离是 2 分米，即 ED’=2 分米。DH⊥OG于点H，则D到直线OG的距离为_________ 分米.

Answer 1

【答案】90 8

【解析】

先利用平行线的性质与等腰三角形的性质证明∠DOG=∠COG，在利用等量代换计算出∠DOG+∠D’OG=∠COD’=90°；先构造Rt△OMD’，再利用全等的性质以及勾股定理计算DH的长．

（1）过点D’作MD’⊥OH于点M，记AB与OH交于点N

∵OD∥AB，OG∥BC

∴∠DOG=∠ANO，∠ANO=∠ABC，∠ACB=∠COG

∴∠DOG=∠ABC

∵AB=AC

∴∠ABC=∠ACB

∴∠DOG=∠ABC=∠ACB=∠COG

∵OD’⊥AC

∴∠COD’=90°

∴∠DOG+∠D’OG=∠COG+∠D’OG=∠COD’=90°

（2）∵DH⊥OG，D’M⊥OG

∴∠OHD=∠OMD’=90°

∴在Rt△OHD中，∠DOG+∠ODH=90°

又∵∠DOG+∠D’OG=90°

∴∠ODH=∠D’OG

∵旋转

∴OD=D’O

在△ODH和△D’OM中

∴△ODH≌△D’OM（AAS）

∴DH=OM

又∵HM=ED’=2

∴DH=OM=OH+HM=OH+2

不妨设OH=x，则DH=x+2

∴在Rt△OHD中，OD=10，

由勾股定理可得：

即：

解得：，（舍去）

∴D到直线OG的距离为DH=x+2=8．

故答案为：90，8．