题目内容
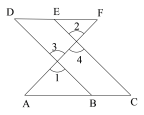
【题目】如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
(1)当BG=2,DH=3时,则GH:HF= ,∠AGH= °;
(2)若BG=3,DH=1,求DF、EG的长;
(3)设BG=x,DH=y,若△ABG∽△FDH,求y与x之间的函数关系式,并求出y的取值范围.

【答案】(1)1:3,90;(2)![]() ;(3)3≤y<4.
;(3)3≤y<4.
【解析】试题分析:(1)根据正方形ABCD的边长为4,BG=2,DH=3,可得CG=2,CH=1,再根据DF∥CG,得出△FDH∽△GCH,根据相似三角形的性质可得GH:HF的值,最后根据勾股定理的逆定理,判定△AGH是直角三角形,且∠AGH=90°即可;
(2)根据正方形ABCD的边长为4,BG=3,DH=1,得出CG=1,CH=3,再根据CG∥DF,CH∥BE,可得△CGH∽△BGE∽△DFH,最后根据相似三角形的性质以及勾股定理,求得DF、EG的长;
(3)根据正方形ABCD的边长为4,BG=x,DH=y,得出CG=4﹣x,CH=4﹣y,由(1)可得,△FDH∽△GCH,而△ABG∽△FDH,进而得出△ABG∽△GCH,根据相似三角形的对应边成比例,可得y与x之间的函数关系式为:y=![]() x2﹣x+4,最后运用二次函数的性质求得3≤y<4即可.
x2﹣x+4,最后运用二次函数的性质求得3≤y<4即可.
试题解析:解:(1)∵正方形ABCD的边长为4,BG=2,DH=3,∴CG=2,CH=1,∵DF∥CG,∴△FDH∽△GCH,∴ ![]() ,∵Rt△GCH中,GH2=CG2+CH2=5,Rt△ABG中,AG2=AB2+BG2=20,Rt△ADH中,AH2=AD2+DH2=25,∴GH2+AG2=AH2,∴△AGH是直角三角形,且∠AGH=90°.
,∵Rt△GCH中,GH2=CG2+CH2=5,Rt△ABG中,AG2=AB2+BG2=20,Rt△ADH中,AH2=AD2+DH2=25,∴GH2+AG2=AH2,∴△AGH是直角三角形,且∠AGH=90°.
故答案为:1:3,90;
(2)∵正方形ABCD的边长为4,BG=3,DH=1,∴CG=1,CH=3,∵CG∥DF,CH∥BE,∴△CGH∽△BGE∽△DFH,∴ ![]() ,即
,即![]() ,解得BE=9,DF=
,解得BE=9,DF=![]() ,∴Rt△BEG中,EG=
,∴Rt△BEG中,EG=![]() =
=![]() =
=![]() ;
;
(3)∵正方形ABCD的边长为4,BG=x,DH=y,∴CG=4﹣x,CH=4﹣y,由(1)可得,△FDH∽△GCH,而△ABG∽△FDH,∴△ABG∽△GCH,∴ ![]() ,即
,即![]() ,∴y与x之间的函数关系式为:y=
,∴y与x之间的函数关系式为:y=![]() x2﹣x+4,∵
x2﹣x+4,∵![]() ,∴4﹣y=
,∴4﹣y=![]() =
= ![]() ,∴当x=﹣
,∴当x=﹣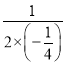 =2时,4﹣y有最大值,且最大值为﹣
=2时,4﹣y有最大值,且最大值为﹣![]() ×4+2=1,∴0<4﹣y≤1,解得3≤y<4.
×4+2=1,∴0<4﹣y≤1,解得3≤y<4.