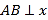题目内容
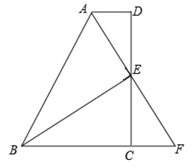
【题目】如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

【答案】(1)见解析;(2)当BC=AF时,四边形ABFC是矩形,理由见解析
【解析】
(1)根据平行四边形的性质得到两角一边对应相等,利用AAS判定△ABE≌△FCE,从而得到AB=CF;
(2)由已知可得四边形ABFC是平行四边形,BC=AF,根据对角线相等的平行四边形是矩形,可得到四边形ABFC是矩形.
(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴![]() ,
, ![]()
∵E为BC的中点
∴BE=EC
∴ △ABE≌△FCE
∴ AB=CF.
(2)解:当BC=AF时,四边形ABFC是矩形.理由如下:
∵AB∥CF,AB=CF
∴四边形ABFC是平行四边形
∵BC=AF
∴四边形ABFC是矩形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)