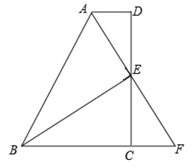
题目内容
【题目】如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.
(1)若AB=6厘米,BE=8厘米,当点P在线段AE上时,求y关于x的函数表达式;
(2)已知点E是BC的中点,当点P在线段ED和AD上时,求y关于x的函数表达式.

【答案】(1)![]() (0<x≤5);(2)当0<x≤5时,
(0<x≤5);(2)当0<x≤5时, ![]() ;当5<x≤8时,y=32﹣4x.
;当5<x≤8时,y=32﹣4x.
【解析】试题分析:(1)AB已知,利用等面积求出P点到AB的距离,三角形面积公式列式,注意求定义域.(2)利用面积求函数关系,因为P点在两条直线上运动,所以函数是一个分段函数,求出在边界点的值,找出函数定义域.
试题解析:
(1)∵四边形ABCD是矩形,∴∠ABE=90°.
又 AB=8,BE=6,
∴AE=![]() =10,设△ABE中,边AE上的高为h,∵S△ABE=
=10,设△ABE中,边AE上的高为h,∵S△ABE= ![]() AEh=
AEh= ![]() ABBE,∴h=
ABBE,∴h= ![]() ,又 AP=2x,∴
,又 AP=2x,∴![]() (0<x≤5).
(0<x≤5).
(2)∵四边形ABCD是矩形,∴∠B=∠C=90°,AB=DC,AD=BC,
∵E为BC中点,
∴BE=EC,∴△ABE≌△DCE,∴AE=DE,当点P运动至点D时,S△ABP=S△ABD,
由题意得![]() x=32﹣4x,解得x=5,
x=32﹣4x,解得x=5,
当点P运动一周回到点A时,S△ABP=0,由题意得32﹣4x=0,解得x=8,
∴AD=2×(8﹣5)=6,∴BC=6,∴BE=3,且AE+ED=2×5=10,
∴AE=5,在Rt△ABE中,AB= ![]() =4,设△ABE中,边AE上的高为h,
=4,设△ABE中,边AE上的高为h,
∵S△ABE= ![]() AEh=
AEh= ![]() ABBE,∴h=
ABBE,∴h= ![]() ,又 AP=2x,
,又 AP=2x,
∴当点P从A运动至点D时,y= ![]() x(0<x≤2.5),
x(0<x≤2.5),
∴y关于x的函数表达式为:当0<x≤5时, ![]()

 科学实验活动册系列答案
科学实验活动册系列答案【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)