Question

【题目】如图，Rt△ABC，∠C=90°，点D为AB上的一点，以AD为直径的⊙O与BC相切于点E，连接AE．

（1）求证：AE平分∠BAC；

（2）若AC=8，OB=18，求BD的长．

Answer 1

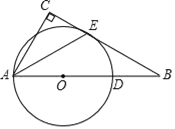
【答案】（1）证明见解析；（2）12.

【解析】试题分析：（1）如图，连接OE．首先证明AC∥OE，推出∠CAE=∠AEO，由OA=OE，推出∠AEO=∠OAE=∠CAE即可证明．

（2）设OE=OA=OD=r，由OE∥AC，得，即，解方程即可．

试题解析：（1）证明：如图，连接OE．

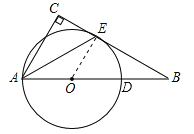
∵BC是⊙O切线，∴OE⊥BC，∴∠OEB=90°，∵∠C=90°，∴∠C=∠OEB=90°，∴AC∥OE，∴∠CAE=∠AEO，∵OA=OE，∴∠AEO=∠OAE=∠CAE，∴AE平分∠CAB；

（2）解：设OE=OA=OD=r，∵OE∥AC，∴ ，即，∴r=6（负根已经舍弃），∴BD=OB﹣OD=18﹣6=12．