题目内容
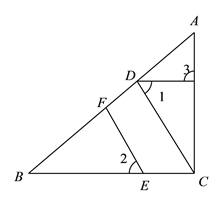
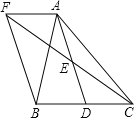
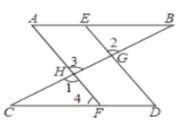
【题目】如图,在矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:根据等角的余角相等,得
∠BAE=∠CEF=∠DFG.
又∠B=∠C=∠D=90°,AE=EF=4,FG=2,
∴△ABE≌△ECF,△ECF∽△FDG.
∴AB=CE,BE=CF,DF:CE=FG:EF=1:2.
∴ ![]() =
= ![]() ,
,
∴DF=FC=BE,
设BE=x,则AB=2x,根据勾股定理,得
x2+4x2=16,
x= ![]() .
.
则矩形ABCD的周长为2(2x+3x)=10x=8 ![]() .
.
故选B.

【考点精析】关于本题考查的勾股定理的概念和相似三角形的判定与性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目