题目内容
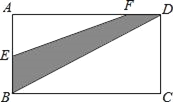
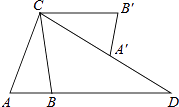
【题目】矩形纸片ABCD中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 . 
【答案】![]()
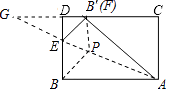
【解析】解:如图所示,设PF⊥CD,
∵BP=FP,
由翻折变换的性质可得BP=B′P,
∴FP=B′P,
∴FP⊥CD,
∴B′,F,P三点构不成三角形,
∴F,B′重合分别延长AE,CD相交于点G,
∵AB∥CD,
∴∠BAG=∠AGD,
∵∠BAG=∠B′AG,
∴∠AGD=∠B′AG,
∴GB′=AB′=AB=5,
∵PB′(PF)⊥CD,
∴PB′∥AC,
∴△ACG∽△PB′G,
∵Rt△ACB′中,AB′=AB=5,AC=3,
∴B′C= ![]() =4,
=4,
∴CB′=5﹣4=1,CG=CB′+B′G=4+5=9,
∴△ACG与△PB′G的相似比为9:5,
∴AC:PB′=9:5,
∵AC=3,
∴PB′= ![]() .
.
所以答案是: ![]() .
.
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目