��Ŀ����
����Ŀ���ڼס������������ĺ����У��ֱ�װ�г���ɫ��������ȫ��ͬ��С�����У�����װ��2������1�������Һ���װ��2������1������
��1��������ҡ�Ⱥ����ȡ��һ��С����С���ǰ�ɫ�ĸ��ʣ�
��2��С����ͬ���̶�������������ҡ�Ⱥ��������һ��С������ɫ��ͬ����С����ʤ������ɫ��ͬ����ͬ����ʤ�������б�������״ͼ�ķ���˵��˭Ӯ�Ŀ����Դ�
���𰸡���1��![]() ����2��ͬ����ʤ��ʤ�Ŀ����Դ�����
����2��ͬ����ʤ��ʤ�Ŀ����Դ�����
��������
��1���ɸ��ʹ�ʽ���ɵó��𰸣�
��2�����б���֪������9�ֵȿ��ܽ����������ɫ����ͬ�Ľ����4�֣���ɫ��ͬ�Ľ����5�֣�P����ɫ����ͬ����![]() ��P����ɫ��ͬ����
��P����ɫ��ͬ����![]() �����ɵó��𰸣�
�����ɵó��𰸣�
�⣺��1������3�ֵȿ��ܽ��������������Ľ����2��
��P����������![]()
��2���������⣬�б����£�
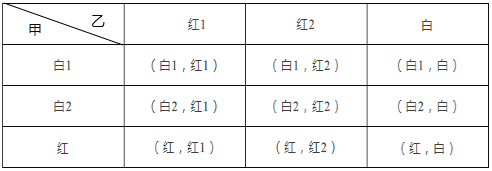
���ϱ���֪������9�ֵȿ��ܽ����������ɫ����ͬ�Ľ����5�֣���ɫ��ͬ�Ľ����4�֣�
��P����ɫ����ͬ����![]() ��P����ɫ��ͬ����
��P����ɫ��ͬ����![]() ����
����![]() ��
��![]() ��
��
��ͬ����ʤ��ʤ�Ŀ����Դ�

��ϰ��ϵ�д�
 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
�����Ŀ