��Ŀ����
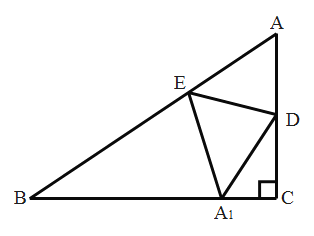
����Ŀ����Rt��ABC�У����ǹ涨��һ����ǵĶԱ���б�ߵı�ֵ��Ϊ�����ǵ�����ֵ��
���磺Rt��ABC�У���C��90������A�ĶԱ�BC��б��AB�ı�ֵ����![]() ���ǡ�A������ֵ�����������������������������ֵ�ٲ鿨���������������£�
���ǡ�A������ֵ�����������������������������ֵ�ٲ鿨���������������£�
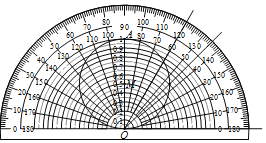
��ͼ����OA��1����OΪԲ�ģ��ֱ���0.05��0.1��0.15��0.2������0.9��0.95��Ϊ�뾶����Բ������OAΪֱ������M���������������ֵ�ٲ鿨�����Զ�����Ӧ������ҵĽ���ֵ�����磺60��������ֵԼ��0.85��0.88֮��ȡֵ��45��������ֵԼ��0.70��0.72֮��ȡֵ�����нǶ�������ֵ��ӽ�0.94���ǣ�������
A.30��B.50��C.40��D.70��
���𰸡�D
��������
�������������ֵ�ٲ鿨����ȡ��Ӧ������ҵĽ���ֵ�ķ������ҵ��Ե�OΪԲ�ġ�0.95Ϊ�뾶�İ�Բ����M�Ľ��㣬��ӽ��ĽǶȼ�Ϊ����.
�⣺��ͼ��֪���Ե�OΪԲ�ġ�0.95Ϊ�뾶�İ�Բ����M�Ľ�����70���ǵ������ϣ���������ֵ��ӽ�0.94����70����.
��ѡ��D��

��ϰ��ϵ�д�
�����Ŀ