题目内容
【题目】如图,![]() 是等边
是等边![]() 的边
的边![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 连
连![]() 接交
接交![]() 于
于![]() ,过
,过![]() 点作
点作![]() 于
于![]() 点.证明下列结论:
点.证明下列结论:
![]()
![]()
![]()

【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)由等边△ABC,DG⊥AC,可求得∠AGD=90°,∠ADG=30°,然后根据直角三角形中,30°角所对的直角边等于斜边的一半,即可证得AG=![]() AD;
AD;
(2)首先过点D作DH∥BC交AC于点H,证得△ADH是等边三角形,又由CE=DA,可利用AAS证得△DHF≌△ECF,继而可得DF=EF;
(3)由△ABC是等边三角形,DG⊥AC,可得AG=GH,即可得S△ADG=S△HDG,又由△DHF≌△ECF,即可证得S△DGF=S△ADG+S△ECF.
证明:(1)∵△ABC是等边三角形,
∴∠A=60°,
∵DG⊥AC,
∴∠AGD=90°,∠ADG=30°,
∴AG=![]() AD;
AD;
(2)过点D作DH∥BC交AC于点H,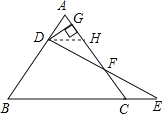
∴∠ADH=∠B,∠AHD=∠ACB,∠FDH=∠E,
∵△ABC是等边三角形,
∴∠B=∠ACB=∠A=60°,
∴∠A=∠ADH=∠AHD=60°,
∴△ADH是等边三角形,
∴DH=AD,
∵AD=CE,
∴DH=CE,
在△DHF和△ECF中,

∴△DHF≌△ECF(AAS),
∴DF=EF
(3)∵△ABC是等边三角形,DG⊥AC,
∴AG=GH,
∴S△ADG=S△HDG,
∵△DHF≌△ECF,
∴S△DHF=S△ECF,
∴S△DGF=S△DGH+S△DHF=S△ADG+S△ECF.

练习册系列答案
相关题目








