题目内容
【题目】(1)课本习题回放:如图①,∠ACB=90°,AC=BC, AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm..求BE的长.
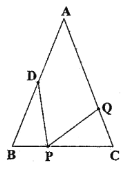
(2)探索证明:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.

【答案】(1)0.8cm;(2)见解析
【解析】
(1)利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质、结合图形解答即可;
(2)根据等角的补角相等得到∠BEA=∠AFC,根据三角形的外角的性质证明∠ABE=∠4,再利用AAS定理证明即可.
(1)∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,∴∠EBC=∠DCA.
在△CEB和△ADC中,∵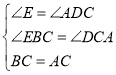 ,∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5.
,∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5.
∵DC=CE﹣DE,DE=1.7,∴DC=2.5﹣1.7=0.8,∴BE=0.8(cm);
(2)∵∠1=∠2,∴∠BEA=∠AFC.
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,∴∠BAC=∠ABE+∠3 ∴∠4=∠ABE.
∵∠BEA =∠AFC,∠ABE=∠4,AB=AC,∴△ABE≌△CAF(AAS)

练习册系列答案
相关题目