题目内容
【题目】已知：AP平分
，点B是射线AP上一定点，点C在直线AM上运动，连接BC．
如图1，
，将
的两边射线BC和BA分别绕点B顺时针旋转
，旋转后角的两边分别与射线AN交于点D和点
当点C在射线AM上时，请直接写出：
和BC之间的数量关系是______；
线段AC，AD和AB之间的数量关系是______．
如果
，将
的两边射线BC和BA分别绕点B顺时针旋转
，旋转后角的两边分别与射线AN交于点D和点E．
如图2，当点C在射线AM上时，请探究线段AC，AD和AB之间的数量关系，写出结论并给予证明；
如图3，当点C在射线AM的反向延长线上时，BC交射线AN于点F，若
，
，请直接写出线段AD和DF的长．
【答案】
；
；
①
，证明见解析；
，
．
【解析】
先判断出
，进而得出
，判断出
≌
，即可得出结论；
先判断出四边形AGBH是正方形，进而得出
，再判断出
，即可得出结论；
同
的方法即可得出结论；
如图3中，作
于G，
于H，
于
由可知，
≌
，
≌
，易知
，
，
，推出
，由
，可得
，设
，则
，
，由
∽
，可得
，求出y即可解决问题．
如图1，
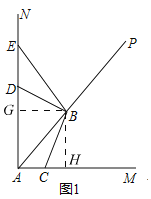
过点B作
于G，
于H，
，
，
，
，
，
是
的平分线，，，
，
，
≌
，
，
；
故答案为；
如图1，由
知，过点B作于G，于H，
，
四边形AGBH是矩形，
由知，
，
矩形AGBH是正方形，
，
，
，
；
故答案为：；
如图2，
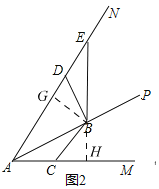
过点B作于G，于H，
，
，
，
，
，
是的平分线，，，
，
，
≌，
，
，
是的平分线，
，
在
中，
，
；
如图3中，
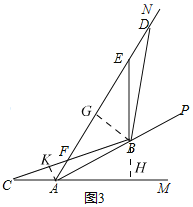
作于G，于H，于K．
由可知，≌，
易证，≌，
易知，，
，
，
，
，
，
，
设，则，，
，
，
∽，
，
，
两边平方，整理得，
，
解得
或
大于AC，舍去
．
即：，．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
