题目内容
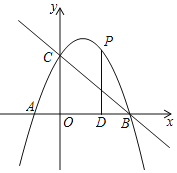
【题目】如图，抛物线
与坐标轴交点分别为
，
，
，作直线BC．
求抛物线的解析式；
点P为抛物线上第一象限内一动点，过点P作
轴于点D，设点P的横坐标为
，求
的面积S与t的函数关系式；
条件同，若
与
相似，求点P的坐标．
【答案】（1）
；（2）
；（3）点P的坐标为
或
【解析】
把
，
，
代入
，利用待定系数法进行求解即可得；
设点P的坐标为
，则
，然后由点A和点B的坐标可得到
，接下来，依据三角形的面积公式求解即可；
当
∽
时，
；当∽
，则
，然后依据比例关系列出关于t的方程求解即可．
把，，代入得：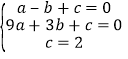
，
解得：
，
，
，
抛物线的解析式为
；
设点P的坐标为，
，，
，
；
当∽时，，即
，
整理得：
，
解得：
或
舍去
，
，
，
点P的坐标为
；
当∽，则，即
，
整理得
，
解得：
或
舍去，
，
，
点P的坐标为
，
综上所述点P的坐标为或
练习册系列答案
阅读快车系列答案
相关题目
