题目内容
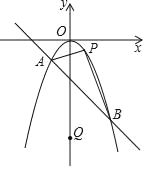
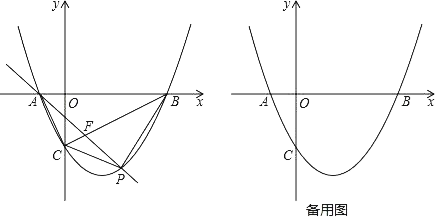
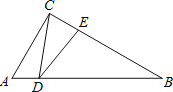
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB边上一个动点(不与点A、B重合),E是BC边上一点,且∠CDE=30°.设AD=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.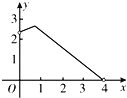 B.
B.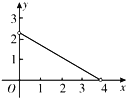 C.
C.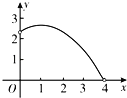 D.
D.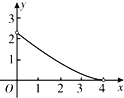
【答案】C
【解析】
根据题意可得出![]()
![]() 然后判断△CDE∽△CBD,继而利用相似三角形的性质可得出y与x的关系式,结合选项即可得出答案.
然后判断△CDE∽△CBD,继而利用相似三角形的性质可得出y与x的关系式,结合选项即可得出答案.
解:∵∠A=60°,AC=2,
∴![]()
![]()
在△ACD中,利用余弦定理可得CD2=AC2+AD2﹣2ACADcos∠A=4+x2﹣2x,
故可得![]() ,
,
又∵∠CDE=∠CBD=30°,∠ECD=∠DCB(同一个角),
∴△CDE∽△CBD,即可得![]()
即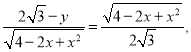
故可得: ![]() 即呈二次函数关系,且开口朝下.
即呈二次函数关系,且开口朝下.
故选C.

练习册系列答案
相关题目